���嗝�n���w'07�N�O����[1]
�ȉ��̊e��ɂ��ꂼ�ꓚ����B
��1�D��ϕ� �����߂�B
�����߂�B ��2�D1����1�i�܂���2�i�̂����ꂩ�ŊK�i������Ƃ��A1����2�i���邱�Ƃ͘A�����Ȃ����̂Ƃ���B15�i�̊K�i�����鏸����͉��ʂ肠�邩�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��1�D�̒�ϕ��͊ȒP�����Ɍ����܂����A���ȏ����x�����z����Z�I��K�v�Ƃ��܂��B2�̐ϕ��ɕ����āA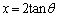 �Ƃ����Ă��ł��܂����A
�Ƃ����Ă��ł��܂����A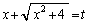 �Ƃ����̂��ł��ȒP�ł�(�u���ϕ�(����3)���Q��)�B
�Ƃ����̂��ł��ȒP�ł�(�u���ϕ�(����3)���Q��)�B ��2�D���܂��l����������悤�ł����A�����ł́A���}�ɐ����Ă������Ƃɂ��܂��B�������ł́A�����l���Ă��܂���@���Ђ�߂��Ȃ��ꍇ�́A���܂�ɖʓ|�Ƃ����̂łȂ�����A�����ȉ�@�����S�m���ł��B
��1�D�܂��A �Ƃ����u�����l���܂�(�u���ϕ����Q��)�B
�Ƃ����u�����l���܂�(�u���ϕ����Q��)�B 2�悵�āA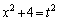 �C���ӂ�������āA
�C���ӂ�������āA
�� 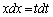
x�F �̂Ƃ��At�F
�̂Ƃ��At�F
���̒u���ɂ��A �ł����A �̐ϕ����c��܂��B
�̐ϕ����c��܂��B
���̐ϕ��́A �Ƃ���(�u���ϕ�(����3)���Q��)�ƁA���ӂ�������āA
�Ƃ���(�u���ϕ�(����3)���Q��)�ƁA���ӂ�������āA �ȏ���A
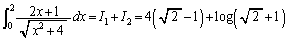 ......[��]
......[��]
��2�D1����1�i����̂��@�C1����2�i����̂��A�ŕ\�����Ƃɂ��܂��B
��ӂ��A�A�͘A�����Ȃ��̂ŁA�e�A�A'�Ƃ������т͂ł��܂���B�A�ƇA�̊Ԃɂ͕K���@������܂��B
�A��6�ȏ�o�Ă���ƁA6�̇A�̊Ԃɇ@��5�ȏ���邱�ƂɂȂ�A17�i�ȏ㏸�邱�ƂɂȂ�̂ŁA�A�̌���0�`5�ł��B
(a) �A��5�̂Ƃ��A�܂��A�A���A�����Ȃ��悤�ɁA�A�ƇA�̊Ԃɇ@��1����4����܂��B
�A�@�A�@�A�@�A�@�A
����ł́A14�i��������Ȃ��̂ŁA����1�@���ǂ����ɒu���Ȃ���Ȃ�Ȃ��̂ł����A�@��u���ʒu�́A���ɇ@���u����Ă���4�J����2�̂߂̇@��u�����A�A�̗��[�A���킹��6�J���̂ǂ����ɂȂ�̂ŁA6�ʂ�B
(b) �A��4�̂Ƃ��A
�A�@�A�@�A�@�A
����ł́A11�i�Ȃ̂ŁA�@4��u���܂����A���ɇ@���u����Ă���3�J���A�A�̗��[�A���킹��5�J���̒�����A�d����������4�J����I��(�d���g�ݍ��킹���Q��)�̂ŁA 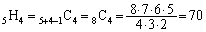 �ʂ�B
�ʂ�B(c) �A��3�̂Ƃ��A
�A�@�A�@�A
����ł́A8�i�Ȃ̂ŁA�@7��u���܂����A���ɇ@���u����Ă���2�J���A�A�̗��[�A���킹��4�J���̒�����A�d����������7�J����I�Ԃ̂ŁA
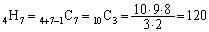 �ʂ�B
�ʂ�B(d) �A��2�̂Ƃ��A
�A�@�A
����ł́A5�i�Ȃ̂ŁA�@10��u���܂����A���ɇ@���u����Ă���1�J���A�A�̗��[�A���킹��3�J���̒�����A�d����������10�J����I�Ԃ̂ŁA
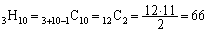 �ʂ�B
�ʂ�B(e) �A��1�̂Ƃ��A�@13��u���܂����A�A�̗��[2�J���̒�����d����������13�J����I�Ԃ̂ŁA
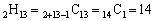 �ʂ�B
�ʂ�B(f) �A��0�̂Ƃ��A�@15�̒u�����́A1�ʂ�B
�ȏ���A �ʂ� ......[��]
�ʂ� ......[��]
�ʉ��@��L����ɇ@��u���Ă��܂��Ƃ����l�������ł��܂��B�A�̌��ɉ����āA�@�̌��́A5�A7�A9�A11�A13�A15�ɂȂ�܂��B
(a) �@��5�̂Ƃ��A�@�Ƈ@�̊ԁA�܂��͗��[�A���킹��6�J���̂ǂ����ɇA��5�u���̂ŁA6�ʂ�B
(b) �@��7�̂Ƃ��A�@�Ƈ@�̊ԁA�܂��͗��[�A���킹��8�J���̂ǂ����ɇA��4�u���̂ŁA �ʂ�B
�ʂ�B (c) �@��9�̂Ƃ��A�@�Ƈ@�̊ԁA�܂��͗��[�A���킹��10�J���̂ǂ����ɇA��3�u���̂ŁA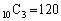 �ʂ�B
�ʂ�B (d) �@��11�̂Ƃ��A�@�Ƈ@�̊ԁA�܂��͗��[�A���킹��12�J���̂ǂ����ɇA��2�u���̂ŁA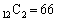 �ʂ�B
�ʂ�B (e) �@��13�̂Ƃ��A�@�Ƈ@�̊ԁA�܂��͗��[�A���킹��14�J���̂ǂ����ɇA��1�u���̂ŁA �ʂ�B
�ʂ�B (f) �@��15�̂Ƃ��A�A�͒u���Ȃ��̂ŁA1�ʂ�B
�ȏ���A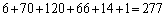 �ʂ� ......[��]
�ʂ� ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B