���嗝�n���w'07�N�O���b[1]
���̊e��ɂ��ꂼ�ꓚ����B
��1�D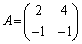 �C
�C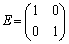 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A 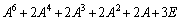 �����߂�B
�����߂�B
��2�D���_1�C2�C����Cn���������m���œ�����Q�[����Ɨ���3��J��Ԃ��B���̂Ƃ��A2��ڂ̓��_��1��ڂ̓��_�ȏ�ł���A�����3��ڂ̓��_��2��ڂ̓��_�ȏ�ƂȂ�m�������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��1�D�́A�n�~���g���E�P�[���[�̒藝���������̏��Z�𗘗p����T�^���ł��B��2�D�́A���܂��l����������悤�ł����A�����ł͎��p�I�ɁA�]�������l���Ă݂܂��B�Ȃ��A�d���g�ݍ��킹�𗘗p����ʉ���t�L���Ă����܂��B
�� 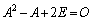 �@����@
�@����@
 �Ƃ����A
�Ƃ����A ���@�Ɠ��^�̑�����
���@�Ɠ��^�̑�����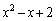 �Ŋ���(�������̏��Z���Q��)�ƁA����
�Ŋ���(�������̏��Z���Q��)�ƁA����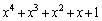 �C�]�肪
�C�]�肪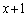 �C����āA
�C����āA �܂��A�@��p����ƁA
 ......[��]
......[��]
��2�D�@1��ځC2��ځC3��ڂ̓��_��x�Cy�Cz�Ƃ���ƁA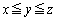 �ƂȂ��m�������߂����킯�ł��B
�ƂȂ��m�������߂����킯�ł��B ���̂܂��ꍇ�̐��𐔂��Ă��ǂ��̂ł����A�]�������l���Ă݂܂��B
�e '�C�܂�e
'�C�܂�e ����
���� '�̗]���ۂ́A�e
'�̗]���ۂ́A�e �܂���
�܂���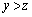 '�ł��B
'�ł��B
�e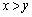 '�Ƃ������ۂł�z�͔C�ӂȂ̂ŁAx�Cy�ɂ��Ă̂ݍl���܂��Bx�Cy�̏o���́A�S����
'�Ƃ������ۂł�z�͔C�ӂȂ̂ŁAx�Cy�ɂ��Ă̂ݍl���܂��Bx�Cy�̏o���́A�S����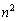 �ʂ肠��܂��B
�ʂ肠��܂��B
�e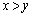 '�Ƃ������ۂƁe
'�Ƃ������ۂƁe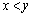 '�Ƃ������ۂƂ͔r���ł���܂����l�Ɋm���炵���A�e
'�Ƃ������ۂƂ͔r���ł���܂����l�Ɋm���炵���A�e �܂���
�܂���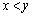 '�Ƃ������ۂ̗]���ۂ́e
'�Ƃ������ۂ̗]���ۂ́e '�ł��B
'�ł��B �e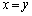 '�Ƃ����o���́An�ʂ肠��܂��B����āA�e
'�Ƃ����o���́An�ʂ肠��܂��B����āA�e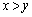 '�ƂȂ�m��
'�ƂȂ�m��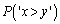 �́A
�́A
�e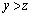 '�Ƃ����m�������l��
'�Ƃ����m�������l��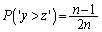
�Ƃ���ŁA�e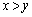 '���e
'���e '�C�܂�e
'�C�܂�e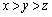 '�ƂȂ�ꍇ�̐��́An�̈قȂ���̂���3��I�ԑg�ݍ��킹�̐��ł����āA
'�ƂȂ�ꍇ�̐��́An�̈قȂ���̂���3��I�ԑg�ݍ��킹�̐��ł����āA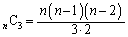 �ʂ�Bx�Cy�Cz�̏o���́A�S����
�ʂ�Bx�Cy�Cz�̏o���́A�S���� �ʂ肠��܂��B
�ʂ肠��܂��B
�e '�ƂȂ�m��
'�ƂȂ�m��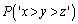 �́A
�́A ���߂�m�� �́A
�́A 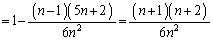 ......[��]
......[��]�ʉ��@x�Cy�Cz�̏o���́A�S����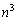 �ʂ肠��܂��B1����n�܂�n�̐�������ׂď����Ă����An�̊e�����̉E��n�J���̂ǂ�����3�{�̋��E������������(1�̐����̉E���ɕ����̋��E������������ł��\��Ȃ�)�A�e���E���̍��ɂ��鐔����x�Cy�Cz�Ƃ���ƁA
�ʂ肠��܂��B1����n�܂�n�̐�������ׂď����Ă����An�̊e�����̉E��n�J���̂ǂ�����3�{�̋��E������������(1�̐����̉E���ɕ����̋��E������������ł��\��Ȃ�)�A�e���E���̍��ɂ��鐔����x�Cy�Cz�Ƃ���ƁA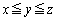 �ƂȂ�1�̏ꍇ����邱�Ƃ��ł��܂��B
�ƂȂ�1�̏ꍇ����邱�Ƃ��ł��܂��B
�e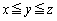 '�ƂȂ�ꍇ�̐��́An�̐����Ƌ��E���̕��ו��𐔂���Ηǂ��̂ł����A1�̍��ɋ��E�������Ă͂����Ȃ��̂ŁA2����n�܂ł�
'�ƂȂ�ꍇ�̐��́An�̐����Ƌ��E���̕��ו��𐔂���Ηǂ��̂ł����A1�̍��ɋ��E�������Ă͂����Ȃ��̂ŁA2����n�܂ł� �̐�����3�{�̋��E����u���ׂ�
�̐�����3�{�̋��E����u���ׂ� �̈ʒu���狫�E����u��3�J����I�ԑg�ݍ��킹�̐��ɓ������A
�̈ʒu���狫�E����u��3�J����I�ԑg�ݍ��킹�̐��ɓ������A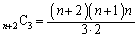 �ʂ肠��܂�(�d���g�ݍ��킹���Q��)�B
�ʂ肠��܂�(�d���g�ݍ��킹���Q��)�B
���߂�m���́A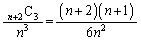 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B