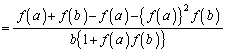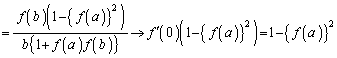���嗝�n���w'07�N�O����[6]
���ׂĂ̎����Œ�`���ꉽ��ł������ł����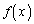 ��
��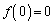 �C
�C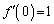 �����A����ɔC�ӂ̎���a�Cb�ɑ���
�����A����ɔC�ӂ̎���a�Cb�ɑ���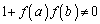 �ł����āA
�ł����āA
�@�@�@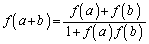
��������B
(1) �C�ӂ̎���a�ɑ��āA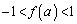 �ł��邱�Ƃ��ؖ�����B
�ł��邱�Ƃ��ؖ�����B (2) 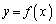 �̃O���t��
�̃O���t��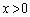 �ŏ�ɓʂł��邱�Ƃ��ؖ�����B
�ŏ�ɓʂł��邱�Ƃ��ؖ�����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ׂĂ̎����Œ�`���ꉽ��ł������ł����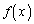 �Ƃ����̂́A
�Ƃ����̂́A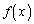 ���A
���A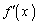 ���A2���ȏ�̑S�Ă̓��������ׂĂ̎���x�ɂ������A���ł���A�Ƃ������Ƃł��B���̖��ł́A�Ȃ��Ȃ��L���ȏ����ł��B
���A2���ȏ�̑S�Ă̓��������ׂĂ̎���x�ɂ������A���ł���A�Ƃ������Ƃł��B���̖��ł́A�Ȃ��Ȃ��L���ȏ����ł��B
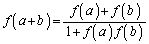 �@����@
�@����@
(1) 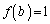 ��������b�����݂���Ɖ��肵�܂��B�@���A�C�ӂ̎���a�ɂ��āA
��������b�����݂���Ɖ��肵�܂��B�@���A�C�ӂ̎���a�ɂ��āA 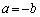 �ƂȂ�a�ɂ��āA
�ƂȂ�a�ɂ��āA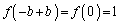 �ƂȂ�
�ƂȂ�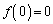 �ɔ�����̂ʼn���͌��ł����āA
�ɔ�����̂ʼn���͌��ł����āA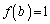 �Ȃ����b�͑��݂��܂���(�w���@�ɂ��ẮA�ؖ��̋Z�I���Q��)�B
�Ȃ����b�͑��݂��܂���(�w���@�ɂ��ẮA�ؖ��̋Z�I���Q��)�B
�܂��A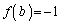 ��������b�����݂���Ɖ��肵�܂��B�@���A�C�ӂ̎���a�ɂ��āA
��������b�����݂���Ɖ��肵�܂��B�@���A�C�ӂ̎���a�ɂ��āA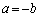 �ƂȂ�a�ɂ��āA
�ƂȂ�a�ɂ��āA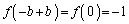 �ƂȂ�
�ƂȂ�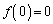 �ɔ�����̂ʼn���͌��ł����āA
�ɔ�����̂ʼn���͌��ł����āA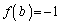 �Ȃ����b�͑��݂��܂���B
�Ȃ����b�͑��݂��܂���B
�ȏ���A�C�ӂ̎���x�ɑ��āA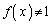 ����
����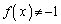 ����
����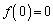 �ł����āA��ӂ���
�ł����āA��ӂ���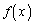 �����ׂĂ̎����ɂ������A���ł��邱�Ƃ���A�C�ӂ̎���a�ɑ��āA
�����ׂĂ̎����ɂ������A���ł��邱�Ƃ���A�C�ӂ̎���a�ɑ��āA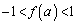 (�ؖ��I)
(�ؖ��I)
(2) �����̒�`���l���Ă݂܂��B�C�ӂ̎���a�ɑ��āA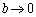 �Ƃ��āA
�Ƃ��āA �Ȃ��Ȃ�A
������ł��B
�ȏ���A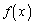 �̓����́A
�̓����́A 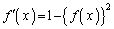 �@����A
�@����A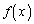 �����ׂĂ̎����ɂ����ĉ���ł������\�Ȃ��Ƃ���A�A���ӂ�x�Ŕ�������ƁA
�����ׂĂ̎����ɂ����ĉ���ł������\�Ȃ��Ƃ���A�A���ӂ�x�Ŕ�������ƁA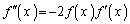 �@����B
�@����B(1)���A���ׂĂ̎���x�ɂ����āA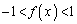 ������A�A���A
������A�A���A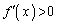 �ł����āA
�ł����āA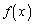 ���P�������Ȋ��ł��B
���P�������Ȋ��ł��B
�]���āA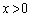 �ɂ����ẮA
�ɂ����ẮA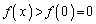
����āA�B���A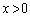 �ɂ����āA
�ɂ����āA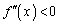
�܂�A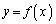 �̃O���t��
�̃O���t��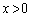 �ŏ�ɓʂɂȂ�܂�(���̉������Q��)�B(�ؖ��I)
�ŏ�ɓʂɂȂ�܂�(���̉������Q��)�B(�ؖ��I)
�NjL�@�A���g����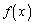 �����߂邱�Ƃ��ł��܂�(�������������Q��)�B
�����߂邱�Ƃ��ł��܂�(�������������Q��)�B
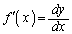 �C
�C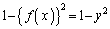 ���A
���A
�� 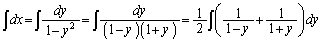
�� 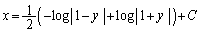
�� 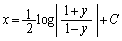
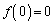 ���A
���A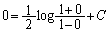
�� 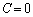
�� 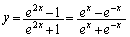
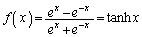 �́A�o�Ȑ����ƌĂ����̈�ł��B��X�̊��̃O���t(4)�̗�7�D���Q�Ƃ��Ă��������B
�́A�o�Ȑ����ƌĂ����̈�ł��B��X�̊��̃O���t(4)�̗�7�D���Q�Ƃ��Ă��������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B