��X�̊��̃O���t(4)�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���̍��ڂ́A�����̌����A���̑����A���̉������Q�Ƃ��Ă��������B
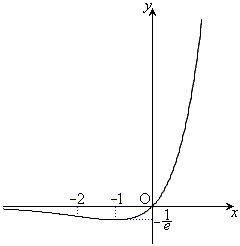 ��1�D
��1�D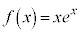
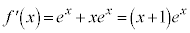 �@(�ς̔����@���Q��)
�@(�ς̔����@���Q��)
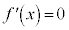 �Ƃ���ƁA
�Ƃ���ƁA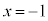
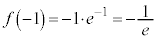 (�ɏ��l)
(�ɏ��l)

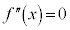 �Ƃ���ƁA
�Ƃ���ƁA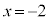
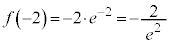
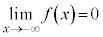 �C
�C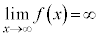
�ȏ���A�����\�͈ȉ��̂悤�ɂȂ�܂��B�O���t�͉E�}�B
���D�O���t�ɂ́A�ϋȓ_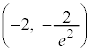 ������܂��B
������܂��B
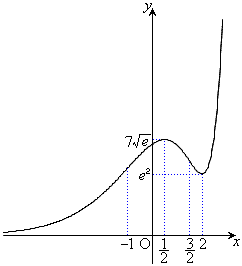 ��2�D
��2�D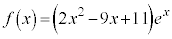
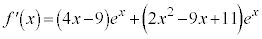 �@(�ς̔����@���Q��)
�@(�ς̔����@���Q��)
�@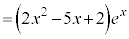 �@����@
�@����@
�@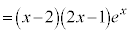
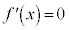 �Ƃ���ƁA
�Ƃ���ƁA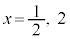
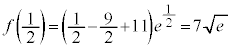 (�ɑ�l)
(�ɑ�l)
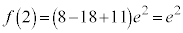 (�ɏ��l)
(�ɏ��l)
�@��������āA
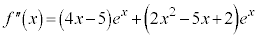
�@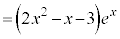
�@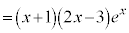
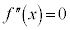 �Ƃ���ƁA
�Ƃ���ƁA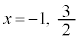
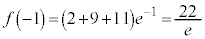
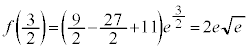
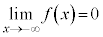 �C
�C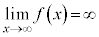
�ȏ���A�����\�͈ȉ��̂悤�ɂȂ�܂��B�O���t�͉E�}�B
| x |
| 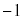 |
| 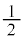 |
| 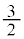 |
| 2 |
|
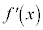 | �{ | �{ | �{ | 0 | �| | �| | �| | 0 | �{ |
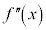 | �{ | 0 | �| | �| | �| | 0 | �{ | �{ | �{ |
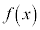 |  | 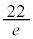 | 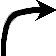 | 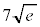 | 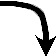 | 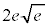 |  | 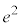 |  |
���D�O���t�ɂ͕ϋȓ_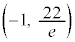 �C
�C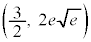 ������܂��B
������܂��B
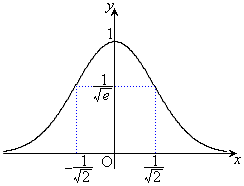 ��3�D
��3�D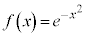
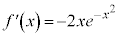 �@(�������̔����@���Q��)
�@(�������̔����@���Q��)
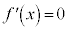 �Ƃ���ƁA
�Ƃ���ƁA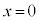
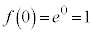 (�ɑ�l)
(�ɑ�l)
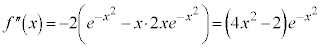 �@(�ς̔����@���Q��)
�@(�ς̔����@���Q��)
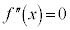 �Ƃ���ƁA
�Ƃ���ƁA
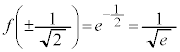
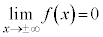
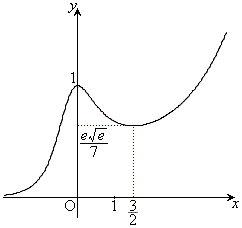
�ȏ���A�����\�͈ȉ��̂悤�ɂȂ�܂��B�O���t�͉E�}�B
| x |
| 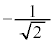 |
| 0 |
| 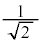 |
|
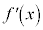 | �{ | �{ | �{ | 0 | �| | �| | �| |
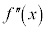 | �{ | 0 | �| | �| | �| | 0 | �{ |
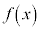 |  | 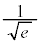 | 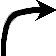 | 1 | 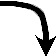 | 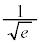 |  |
���D�O���t�ɂ͕ϋȓ_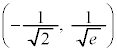 �C
�C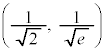 ������܂��B
������܂��B
 ��4�D
��4�D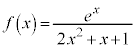
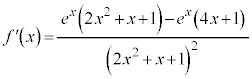 �@(���̔����@���Q��)
�@(���̔����@���Q��)
�@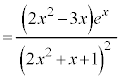
�@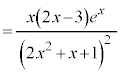
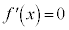 �Ƃ���ƁA
�Ƃ���ƁA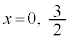
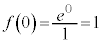 (�ɑ�l)
(�ɑ�l)
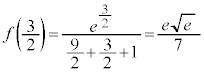 (�ɏ��l)
(�ɏ��l)
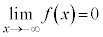 �C
�C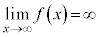
�����\�͈ȉ��̂悤�ɂȂ�܂��B
���D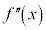 �͕��G�ɂȂ�̂ŏȗ����܂����B
�͕��G�ɂȂ�̂ŏȗ����܂����B
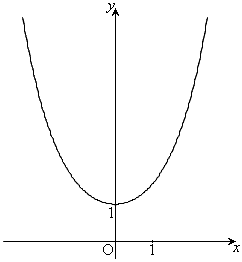 ��5�D
��5�D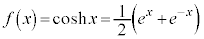
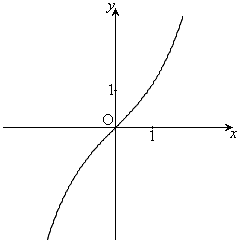 ��6�D
��6�D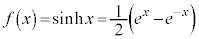
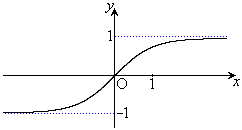 ��7�D
��7�D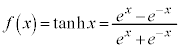
��L��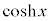 �C
�C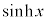 �C
�C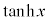 ���܂Ƃ߂đo�Ȑ����ƌ����܂��B�O�p���Ɨގ��̐����������Ă��܂�(�O�p���̂��Ƃ��~���Ƃ������܂�)�B
���܂Ƃ߂đo�Ȑ����ƌ����܂��B�O�p���Ɨގ��̐����������Ă��܂�(�O�p���̂��Ƃ��~���Ƃ������܂�)�B
�E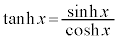
�E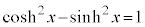
�� 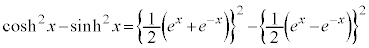
�@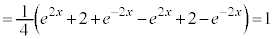
�E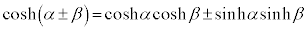 (��������)
(��������)
�� 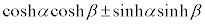
�@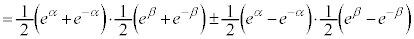
�@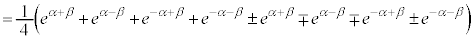
�@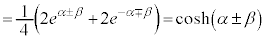 �@(��������)
�@(��������)
�E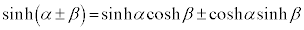 (��������)
(��������)
�� 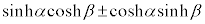
�@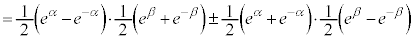
�@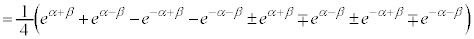
�@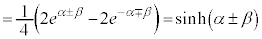 �@(��������)
�@(��������)
�Ȃ��A�o�Ȑ����ƎO�p���ŗގ��̐����������ƌ����ƁA�I�C���[�̌����F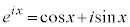 �ɂ��A�O�p���͎w���������̎w����(���Z�͈̔͊O)��p���āA�ȉ��̂悤�ɏ����邩��ł��B
�ɂ��A�O�p���͎w���������̎w����(���Z�͈̔͊O)��p���āA�ȉ��̂悤�ɏ����邩��ł��B
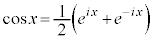 �C
�C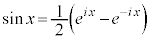 �C
�C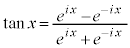
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 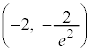 ������܂��B
������܂��B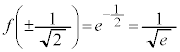
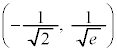 �C
�C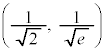 ������܂��B
������܂��B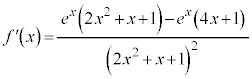 �@(���̔����@���Q��)
�@(���̔����@���Q��)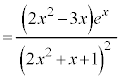
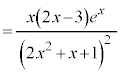
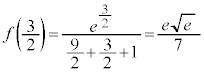 (�ɏ��l)
(�ɏ��l)