���嗝�n���w'09�N��[5]
xy���ʏ�Ō��_���ɁAx���̐��̕������n���Ƃ���ɍ��W�Ɋւ��āA�ɕ�����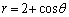 (
(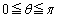 )�ɂ��\�����Ȑ���C�Ƃ���BC��x���Ƃň͂܂ꂽ�}�`��x���̂܂���1��]���ē����闧�̂̑̐ς����߂�B
)�ɂ��\�����Ȑ���C�Ƃ���BC��x���Ƃň͂܂ꂽ�}�`��x���̂܂���1��]���ē����闧�̂̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�P�Ȃ���ς̌v�Z���ł��B���̖��͗��Ƃ��܂���B
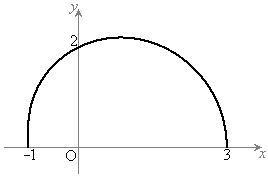 �Ȑ�C�͉E�}�̂悤�Ȍ`�����Ă��܂��B
�Ȑ�C�͉E�}�̂悤�Ȍ`�����Ă��܂��B
�Ȑ�C��̓_�̍��W�́Axy���W�n�ŁA
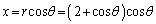 �@����@
�@����@
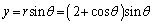 �@����A
�@����A
���Aθ ��0����π�܂œ����ƁA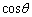 ��1����
��1����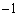 �܂œ����Ax��3����
�܂œ����Ax��3����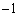 �܂ŒP���Ɍ������܂��B
�܂ŒP���Ɍ������܂��B
�]���āA���߂�̐�V�́A
�ŗ^�����܂��B�@��p���āAx�̐ϕ���θ �̐ϕ��ɕς���(�u���ϕ����Q��)�ƁA�@���A
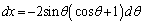 �Cx�F
�Cx�F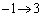 �̂Ƃ��Aθ�F
�̂Ƃ��Aθ�F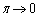
�A���A
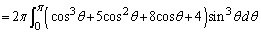
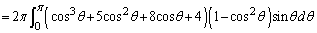
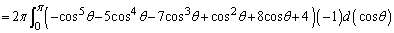
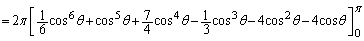 �@(������̂Ƃ���͏�����)
�@(������̂Ƃ���͏�����)
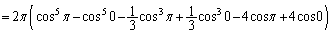
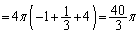 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B