���嗝�n���w'09�N��[6]
a��b���݂��ɑf�A���Ȃ킿1�ȊO�̌��������Ȃ����̐����Ƃ��A�����a�͊�Ƃ���B���̐���n�ɑ��Đ��� �C
�C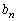 ��
�� ���݂����悤�ɒ�߂�Ƃ��A����(1)�C(2)�������B������
���݂����悤�ɒ�߂�Ƃ��A����(1)�C(2)�������B������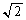 ���������ł��邱�Ƃ͏ؖ��Ȃ��ɗp���Ă悢�B
���������ł��邱�Ƃ͏ؖ��Ȃ��ɗp���Ă悢�B
(1) 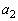 �͊�ł���A
�͊�ł���A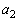 ��
��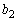 �݂͌��ɑf�ł���B
�݂͌��ɑf�ł���B (2) ���ׂĂ�n�ɑ��āA �͊�ł���A
�͊�ł���A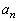 ��
�� �݂͌��ɑf�ł���B
�݂͌��ɑf�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(2)�́A�P�������w�I�A�[�@�ł�낤�Ƃ��Ă����܂��s���܂���B�����ł́A�A���Q�����ɏ]������3���ԑQ�����ɂ��]�����Ƃ𗘗p���A�O2�����肵�Ď����`�̐��w�I�A�[�@���l���邱�Ƃɂ��܂��B�Ȃ��A�������Q�Ƃ��Ă��������B
�܂��AA�CB�CC�CD���L�����ł���Ƃ��A
�ł���A
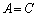 ����
���� 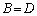
�ɂ����āA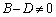 �Ɖ��肷��ƁA
�Ɖ��肷��ƁA
�ƂȂ��Ė�����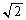 ���L�����ɓ������Ȃ�A�Ƃ����s��������̂ŁA
���L�����ɓ������Ȃ�A�Ƃ����s��������̂ŁA
����āA(��)�����藧���܂��B
(1) 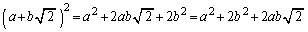
����āA
 �C
�C �͐����Ȃ̂ŁA(��)���A
�͐����Ȃ̂ŁA(��)���A �C
�C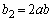
�ƂȂ�܂��B�����ŁA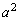 �͊�A
�͊�A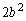 �͋����Ȃ̂ŁA
�͋����Ȃ̂ŁA �͊�ł��B
�͊�ł��B
 ��
��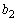 ������d (
������d ( )�����Ƃ���ƁAp�Cq�𐳂̐����Ƃ��āA
)�����Ƃ���ƁAp�Cq�𐳂̐����Ƃ��āA 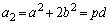 �@����@
�@����@
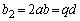 �@����A
�@����A�Ƃ������Ƃ��ł��܂��B�܂��A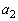 �͊�Ȃ̂�d�͊�ł��B
�͊�Ȃ̂�d�͊�ł��B
�A��� �C������@�~a�ɑ�����āA
�C������@�~a�ɑ�����āA ������Ad��a�̖ł��B�܂��A�@���A
�E�ӂ́A�d�̔{����b��d�̔{���ɂȂ�Ad��a�Cb�̌��ɂȂ�܂��B��ӂ��Aa�Cb��1�ȊO�̌��������Ȃ��̂ŁA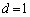 �Ɍ����A
�Ɍ����A �C
�C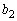 �݂͌��ɑf�ł��B
�݂͌��ɑf�ł��B
(2) �܂��A(1)�ɏK���ĕ��ʂɐ��w�I�A�[�@�łł��Ȃ����l���Ă݂܂��B
 �̂Ƃ��́A
�̂Ƃ��́A �C
�C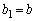 �ŁA
�ŁA �͊�ł���A
�͊�ł���A ��
�� �݂͌��ɑf�ł��B
�݂͌��ɑf�ł��B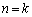 �̂Ƃ��A
�̂Ƃ��A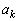 ����ł����āA
����ł����āA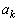 �C
�C ���݂��ɑf�ł���Ɖ��肵�܂��B
���݂��ɑf�ł���Ɖ��肵�܂��B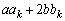 �C
�C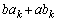 �͐����Ȃ̂ŁA
�͐����Ȃ̂ŁA �C
�C
�ƂȂ�܂��B�����ŁA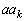 �͊��
�͊�� �͋����Ȃ̂�
�͋����Ȃ̂�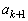 ����ł��B
����ł��B
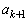 ��
�� ������d (
������d ( )�����Ƃ���ƁAd�͊�ł��Bp�Cq�𐮐��Ƃ��āA
)�����Ƃ���ƁAd�͊�ł��Bp�Cq�𐮐��Ƃ��āA 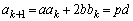 �@����B
�@����B
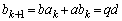 �@����C
�@����C�Ƃ������Ƃ��ł��܂��B
�B�~a�|�C�~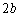 ���A
���A �C�~a�|�B�~b���A
�������A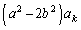 �C
�C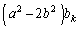 �͌���d�������܂��B
�͌���d�������܂��B
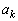 �C
�C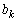 �͉���ɂ��݂��ɑf�Ȃ̂ŁAd��
�͉���ɂ��݂��ɑf�Ȃ̂ŁAd�� �̖@����D�@�Ƃ������ƂɂȂ�܂����A���ꂾ���ł͏����s���ŁA
�̖@����D�@�Ƃ������ƂɂȂ�܂����A���ꂾ���ł͏����s���ŁA �Ɍ���A�Ƃ������Ƃ������܂���B
�Ɍ���A�Ƃ������Ƃ������܂���B ������(1)�̈Ӗ����l���Ă݂܂��B(1)�ł́A �̏ꍇ���������킯�ŁA
�̏ꍇ���������킯�ŁA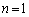 �̏ꍇ��
�̏ꍇ��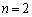 �̏ꍇ�ɂ��Ă͊��Ɏ����Ă���킯�ł��B
�̏ꍇ�ɂ��Ă͊��Ɏ����Ă���킯�ł��B
����ŁA�B�C�C�ɂ��A����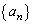 �C
�C �̘A���Q�������^�����܂����A�A���Q�����ɏ]������́A3���ԑQ�����F
�̘A���Q�������^�����܂����A�A���Q�����ɏ]������́A3���ԑQ�����F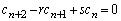 (r�Cs�͒萔)�ɂ��]���܂��B3���ԑQ�����𗘗p����ƁA
(r�Cs�͒萔)�ɂ��]���܂��B3���ԑQ�����𗘗p����ƁA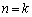 �̏ꍇ�A
�̏ꍇ�A �̏ꍇ�����肵�āA
�̏ꍇ�����肵�āA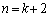 �̏ꍇ���A�Ƃ����`�̐��w�I�A�[�@�����p�ł������ł��B
�̏ꍇ���A�Ƃ����`�̐��w�I�A�[�@�����p�ł������ł��B
�܂��A3���ԑQ���������܂��B
����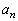 �C
�C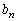 ���A
���A 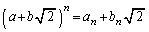 �@����E
�@����E�ɂ���Ē�܂�Ƃ��A��L�ɂ������܂������A
���A
�Ƃ����A���Q�����������܂��B���̂Ƃ��A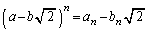 �Ɖ��肷��ƁA
�Ɖ��肷��ƁA �ƂȂ�̂ŁA �ƂȂ�A���ׂĂ̎��R��n�ɂ��āA
�ƂȂ�A���ׂĂ̎��R��n�ɂ��āA  �@����F
�@����F�����藧���܂��B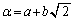 �C
�C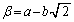 �Ƃ����ƁA
�Ƃ����ƁA
�E�{�F���A �@����G
�@����G
�E�|�F���A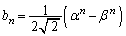 �@����H3���ԑQ�����F
�@����H3���ԑQ�����F
�̈�ʍ� �́A�����������F
�́A�����������F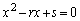 ���قȂ�2������α�Cβ�����Ƃ�(
���قȂ�2������α�Cβ�����Ƃ�( �C
�C )�A
)�A �̌`�ɕ\���邱�Ƃ��v���o���ƁA
 �C
�C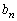 �̏ꍇ�ɂ́A
�̏ꍇ�ɂ́A ���Aα�Cβ �́A2���������F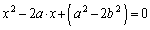 ��2���Ȃ̂ŁA3���ԑQ�����́A
��2���Ȃ̂ŁA3���ԑQ�����́A 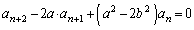 �@����I
�@����I
 �@����J
�@����J�Ƃ����`�ɂȂ肻���ł��B�G��p���āA

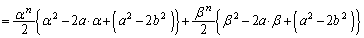
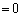 �@(�� α�Cβ �́A2���������F
�@(�� α�Cβ �́A2���������F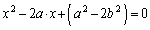 ��2��)
��2��)�ƂȂ�A�I�����藧���܂��B�J���H��p���ē��l�Ɏ����܂��B
���x�́A���w�I�A�[�@�̘g�g�݂�ς��āA
 �̂Ƃ��́A
�̂Ƃ��́A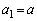 �C
�C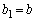 ��
�� �͊�ł���A
�͊�ł���A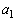 ��
��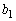 �݂͌��ɑf�A�܂��A(1)���A
�݂͌��ɑf�A�܂��A(1)���A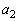 �͊�ł���A
�͊�ł���A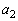 ��
��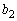 �݂͌��ɑf�ł��B
�݂͌��ɑf�ł��B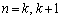 �̂Ƃ��A
�̂Ƃ��A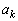 �C
�C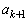 �͊�ł���A
�͊�ł���A �C
�C ���݂��ɑf�A
���݂��ɑf�A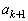 ��
��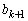 ���݂��ɑf���Ɖ��肵�܂��B
���݂��ɑf���Ɖ��肵�܂��B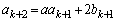 �@����K
�@����K
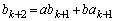 �@����L
�@����L�K�ɂ����āA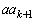 �͊�A
�͊�A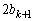 �͋����Ȃ̂�
�͋����Ȃ̂� �͊�ł��B�܂��A
�͊�ł��B�܂��A �C
�C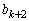 �̌���d�Ƃ���ƁAd�͊�ł����āA��L�̇D�̂Ƃ��Ɠ��l�ɂ��āA
�̌���d�Ƃ���ƁAd�͊�ł����āA��L�̇D�̂Ƃ��Ɠ��l�ɂ��āA
�K�~a�|�L�~ ���A
���A
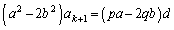
�L�~a�|�K�~b���A
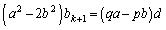
�D�ł������悤�ɁAd�́A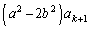 �C
�C �̌��ŁA
�̌��ŁA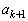 �C
�C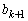 ���݂��ɑf�ł���Ƃ�������ɂ��Ad��
���݂��ɑf�ł���Ƃ�������ɂ��Ad��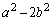 �̖ƂȂ�Ar�𐮐��Ƃ��āA
�̖ƂȂ�Ar�𐮐��Ƃ��āA  �@����M
�@����M�Ƃ����܂��B
�I�ɂ��ƁA
���̉E�ӂ�d�̔{���Ȃ̂ŁA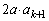 ��d�̔{���ł��B
��d�̔{���ł��B
���l�ɇJ���A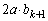 ��d�̔{���ł��B
��d�̔{���ł��B
����ɂ��A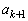 ��
��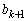 �݂͌��ɑf�ł���Ad��
�݂͌��ɑf�ł���Ad��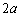 �̖ł����Ċ�Ȃ̂ŁAd��a�̖ƂȂ�As�𐮐��Ƃ��āA
�̖ł����Ċ�Ȃ̂ŁAd��a�̖ƂȂ�As�𐮐��Ƃ��āA �Ƃ����܂��B�M�ɑ������ƁA
������Ad�́A��Ȃ̂�b�̖ŁAa�Cb�̌��ƂȂ�A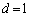 �Ɍ����܂��B
�Ɍ����܂��B
�܂�A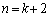 �̂Ƃ����A
�̂Ƃ����A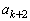 �͊�ł����āA
�͊�ł����āA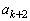 �C
�C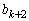 �݂͌��ɑf�ł��B
�݂͌��ɑf�ł��B ����āA���w�I�A�[�@�ɂ��A���ׂĂ�n�ɑ��āA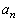 �͊�ł���A
�͊�ł���A ��
��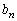 �݂͌��ɑf�ł��B
�݂͌��ɑf�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B