���嗝�n���w'12�N[2]
���l�ʑ�OABC�ɂ����āA�_P�CQ�CR�����ꂼ���OA�COB�COC��ɂƂ�B�������AP�CQ�CR�͎l�ʑ�OABC�̒��_�Ƃ͈قȂ�Ƃ���B��PQR�����O�p�`�Ȃ�A3��PQ�CQR�CRP�͂��ꂼ��3��AB�CBC�CCA�ɕ��s�ł��邱�Ƃ��ؖ�����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��ԃx�N�g����p���ĉ������܂��B
OABC�����l�ʑ̂ł��邱�Ƃ���A
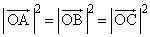 (
(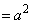 �Ƃ����܂�)�C
�Ƃ����܂�)�C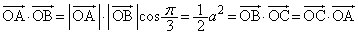 �@����@�@(�������Q��)
�@����@�@(�������Q��) �C
�C �C
�C �Ƃ��āA
�Ƃ��āA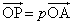 �C
�C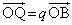 �C
�C �Ƃ������Ƃ��ł��܂��B
�Ƃ������Ƃ��ł��܂��B
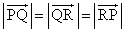 ���A
���A
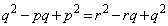 ����
���� 
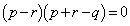 ����
���� 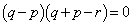
�h �܂���
�܂���  �h ���� �h
�h ���� �h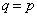 �܂���
�܂��� 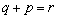 �h
�h
������A�ȉ���3�ʂ�̏ꍇ�����蓾�܂��B
(i) 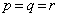 �̂Ƃ��A
�̂Ƃ��A ���A3��PQ�CQR�CRP�͂��ꂼ��3��AB�CBC�CCA�ɕ��s�ł��B
(ii)  ����
���� 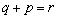 �̂Ƃ��A
�̂Ƃ��A 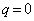 �ƂȂ�AO��Q����v����̂ő�ӂɔ����܂��B
�ƂȂ�AO��Q����v����̂ő�ӂɔ����܂��B(iii)  ����
���� 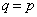 �̂Ƃ��A
�̂Ƃ��A 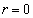 �ƂȂ�AO��R����v����̂ő�ӂɔ����܂��B
�ƂȂ�AO��R����v����̂ő�ӂɔ����܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B