���嗝�n���w'12�N[6]
���������n���ďo���ڂ�����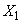 �C
�C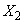 �C����C
�C����C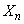 �Ƃ���B����ɁA
�Ƃ���B����ɁA
�ɂ����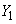 �C
�C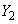 �C����C
�C����C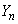 ���߂�B
���߂�B
�ƂȂ�m��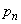 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��蕶�����ăM���b�Ƃ��܂����A��蕶�̕s���������藧���ۂ̗]���ۂ��l���A�����2�̏ꍇ�ɕ����čl����ƁA���̃J���N���������Ă��܂��B
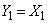 �C
�C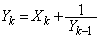 (
(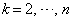 )�@���(��)
)�@���(��)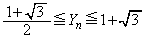 �@���(����)
�@���(����)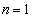 �̂Ƃ��A
�̂Ƃ��A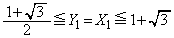 �ƂȂ�̂́A
�ƂȂ�̂́A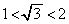 ���A
���A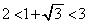 �C
�C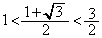 �Ȃ̂ŁA
�Ȃ̂ŁA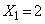 �̂Ƃ������ł��B
�̂Ƃ������ł��B
�]���āA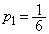 �@����@
�@����@
������(��)���g����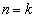 �̂Ƃ��̏���
�̂Ƃ��̏���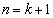 �̂Ƃ��̏��l���邱�ƂɂȂ�܂��B
�̂Ƃ��̏��l���邱�ƂɂȂ�܂��B
(����)��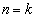 �Ƃ����s�����ƁA
�Ƃ����s�����ƁA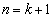 �Ƃ����s�������l���A
�Ƃ����s�������l���A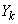 �͈̔͂�
�͈̔͂�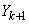 �ׂ͈̔͂邱�ƂɂȂ�܂��B�����ŁA
�ׂ͈̔͂邱�ƂɂȂ�܂��B�����ŁA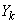 �͈̔͂ɂ��āA�肪����Ă������Ƃɂ��܂��B
�͈̔͂ɂ��āA�肪����Ă������Ƃɂ��܂��B
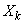 �͂�������̖ڂȂ̂�1����6�̂����ꂩ�ł��B(��)���A
�͂�������̖ڂȂ̂�1����6�̂����ꂩ�ł��B(��)���A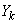 �͂�������̖ڂ����͂��ɑ傫�Ȑ��ŁA
�͂�������̖ڂ����͂��ɑ傫�Ȑ��ŁA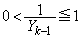 �ƂȂ肻���ł��B
�ƂȂ肻���ł��B
n�����R���̂Ƃ��A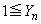 �ł��邱�Ƃ��\�z���A��������w�I�A�[�@�Ŏ����Ă������Ƃɂ��܂��B
�ł��邱�Ƃ��\�z���A��������w�I�A�[�@�Ŏ����Ă������Ƃɂ��܂��B
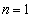 �̂Ƃ��A
�̂Ƃ��A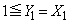 �ł��B
�ł��B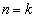 �̂Ƃ��A
�̂Ƃ��A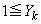 �Ɖ��肷��ƁA
�Ɖ��肷��ƁA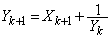 �C
�C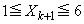 �C
�C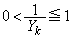 ���A
���A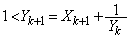 �ł��B
�ł��B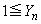 �@����A�@�ł��B
�@����A�@�ł��B
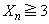 �̂Ƃ��A
�̂Ƃ��A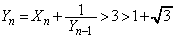 ���A
���A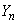 ������(��)�������Ƃ͂���܂���B�܂�A
������(��)�������Ƃ͂���܂���B�܂�A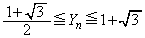 �����̂́A
�����̂́A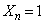 �̂Ƃ����A
�̂Ƃ����A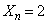 �̂Ƃ������ł��B
�̂Ƃ������ł��B
���������n��������A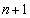 �������l���܂��B
�������l���܂��B
n�����Ƃ��A(����)����������Ă���Ƃ��ƁA��������Ă��Ȃ��Ƃ��ɕ����Ē��ׂ܂��B
(1) ���������n�����Ƃ��A(����)����������Ă����Ƃ��܂��B�����Ȃ��m����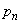 �ł��B���̂Ƃ��A
�ł��B���̂Ƃ��A 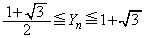 �C
�C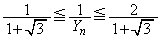
�ł����A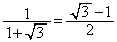 �C
�C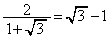 �Ȃ̂ŁA
�Ȃ̂ŁA 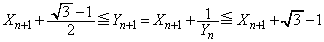 �@����B
�@����B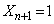 (�m��
(�m��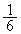 )�̂Ƃ��A�B�́A
)�̂Ƃ��A�B�́A�ƂȂ�A����(����)�͕K����������܂��B�@����C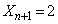 (�m��
(�m��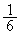 )�̂Ƃ��A�B�́A
)�̂Ƃ��A�B�́A �ƂȂ�A����(����)�͕K����������܂��B�@����D
(2) ���������n�����Ƃ��A(����)����������Ă��Ȃ��Ƃ��܂��B�����Ȃ�m����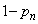 �ł��B���̂Ƃ��A
�ł��B���̂Ƃ��A 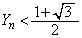 �܂���
�܂���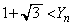
�ł����A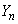 �͈̔͂�2�ɕ�����Ă���̂ŁA�ʁX�ɍl���܂��B
�͈̔͂�2�ɕ�����Ă���̂ŁA�ʁX�ɍl���܂��B (i) 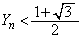 �̂Ƃ��A�A���l�����āA
�̂Ƃ��A�A���l�����āA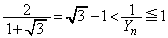 �C����āA
�C����āA 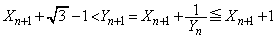 �@����E
�@����E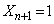 (�m��
(�m��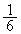 )�̂Ƃ��A�E�́A
)�̂Ƃ��A�E�́A�ƂȂ�A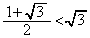 ���A����(����)�͕K����������܂��B�@����F
���A����(����)�͕K����������܂��B�@����F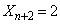 (�m��
(�m��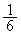 )�̂Ƃ��A�E�́A
)�̂Ƃ��A�E�́A �ƂȂ�A����(����)�͖�������܂���B
(ii) 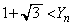 �̂Ƃ��A�A���l�����āA
�̂Ƃ��A�A���l�����āA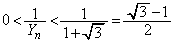 �C����āA
�C����āA 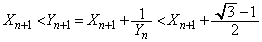 �@����G
�@����G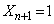 (�m��
(�m��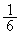 )�̂Ƃ��A�G�́A
)�̂Ƃ��A�G�́A�ƂȂ�A����(����)�͖�������܂���B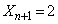 (�m��
(�m��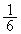 )�̂Ƃ��A�G�́A
)�̂Ƃ��A�G�́A �ƂȂ�A����(����)�͕K����������܂��B�@����H
��L�ŇC�C�D���N����m����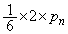 �C�F���N����m���́A
�C�F���N����m���́A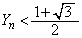 �ƂȂ�m����
�ƂȂ�m����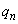 �Ƃ���
�Ƃ���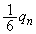 �ł��B�H���N����m���́A
�ł��B�H���N����m���́A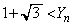 �ƂȂ�m����
�ƂȂ�m����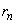 �Ƃ���
�Ƃ���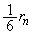 �ł��B
�ł��B
��L�̌������A���������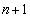 �����Ƃ��A
�����Ƃ��A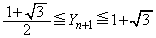 �ƂȂ�ꍇ�́A�C�C�D�C�F�C�H�̂����ꂩ�Ɍ����܂��B�]���āA�����m��
�ƂȂ�ꍇ�́A�C�C�D�C�F�C�H�̂����ꂩ�Ɍ����܂��B�]���āA�����m��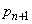 �́A
�́A
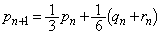 �@����I
�@����I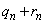 �́A
�́A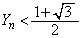 �܂���
�܂���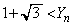 �ƂȂ鎖�ۂ̊m���ł����A���̎��ۂ�
�ƂȂ鎖�ۂ̊m���ł����A���̎��ۂ�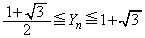 �ƂȂ鎖�ۂ��]�����ł��B����āA
�ƂȂ鎖�ۂ��]�����ł��B����āA
������A�I�́A
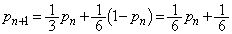 �@����J
�@����J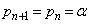 �Ƃ��āA
�Ƃ��āA
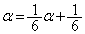 �@����K�@��
�@����K�@�� 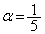
����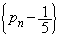 �́A�@���A�����F
�́A�@���A�����F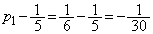 �C����F
�C����F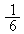 �̓��䐔��ł��B
�̓��䐔��ł��B
����āA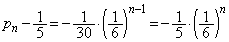
�� 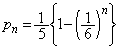 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 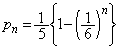 ......[��]
......[��]