京大理系数学'13年[4]
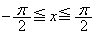における
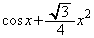の最大値を求めよ。ただし
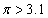および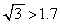
が成り立つことは証明なしに用いてよい。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 数値の評価があるとはいえ、平凡な微分の問題です。
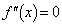とすると、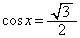
，
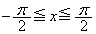においては、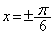
これで、以下の増減表が得られます(関数の増減を参照)。
，
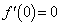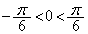なので、
，
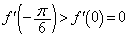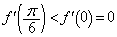です。
従って、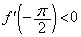
より、方程式
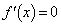は
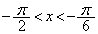の範囲にただ一つの解α (
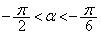)をもちます。また、
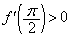より、方程式
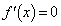は
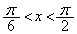の範囲にただ一つの解β (
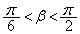，実は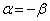
です)をもちます。
結局、方程式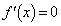
は、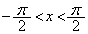
の範囲に、3つの解、α，0，βをもちます。
，
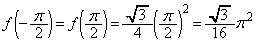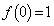
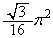と1を比較すると、
よって、求める最大値は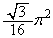
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
