京大理系数学'13年[5]
xy平面内で、y軸上の点Pを中心とする円Cが2つの曲線
とそれぞれ点A，点Bで接しているとする。さらに△PABはAとBがy軸に関して対称な位置にある正三角形であるとする。このとき3つの曲線C，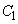
，
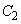で囲まれた部分の面積を求めよ。
ただし、2つの曲線がある点で接するとは、その点を共有し、さらにその点において共通の接線をもつことである。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 円Cと、曲線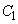
，曲線
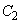とが接するとき、円の中心と接点を結ぶ半径は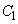、曲線
，曲線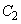
の法線になります。
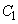と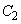
とはy軸に関して対称です。さらに円Cもy軸に関して対称です。従って、接点AとBもy軸に関して対称です。
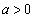として、Aの座標を
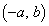とすると、Bの座標は
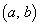となります。△PABが正三角形であることから、円の中心Pのy座標cは、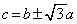
：
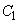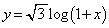について、定義域は
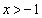であって、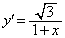
(微分の公式を参照)
点Aにおける接線の傾きは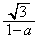
点Aにおける法線の傾きが直線PAの傾きに一致することから、 ∴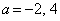 
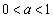より不適。 点Bにおける接線の傾きは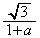
点Bにおける法線の傾きが直線PBの傾きに一致することから、 半径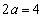
の円の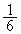
から、1辺4の正三角形の面積を引いた面積
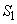は、
線分ABとx軸，2直線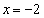
，
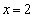で囲まれた長方形の面積
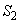は、
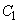とx軸，直線
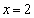で囲まれる部分の面積
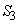は、
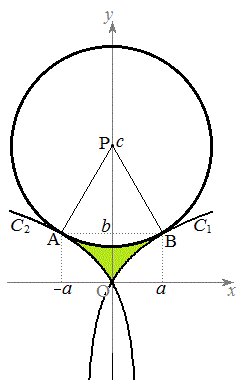
求める面積(右図黄緑色着色部)は、
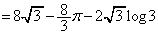......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
：
， 
：
が
上の点であるとき、
(
，
)
が
上の点であるとき、
(
，
)
より、
，
上の点です。
