���嗝�n���w'20�N�O��[5]
�c4�A��4�̃}�X�ڂ̂��ꂼ���1�C2�C3�C4�̐��������Ă����B���̃}�X�ڂ̉��̕��т��s�Ƃ����A�c�̕��т��Ƃ����B�ǂ̍s�ɂ��A�ǂ̗�ɂ�����������1������Ȃ�������͉��ʂ肠�邩���߂�B���}�͂��̂悤�ȓ������1��ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Ώ̐����l�����ďꍇ�̐��𐔂��܂��B
(i) �܂��A1�s�ڂ�4�����̓�����́A�قȂ�4�̂��̂������ƂȂ�A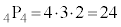 �ʂ�B�@����@
�ʂ�B�@����@
1�C2�C3�C4�̐��������ւ��čl����Ƃ��̑Ώ̐����A����24�ʂ�̊e1�ʂ�ɂ��āA2�s�ڈȍ~�̐����̓�����́A����������܂��B�����ŁA24�ʂ�̂�����1�ʂ�A1�s�ڂɗႦ�A1�C2�C3�C4�Ɠ��ꂽ�ꍇ���l���܂��B
(ii) 2�s�ڂ́A1��ڂɂ�1�����邱�Ƃ��ł��Ȃ��̂ŁA1������ʒu�́A2��ځA3��ځA4��ڂ�3�ʂ肠��܂��B�@����A
2�C3�C4�̐��������ւ��čl����Ƃ��̑Ώ̐����A����3�ʂ�̊e1�ʂ�ɂ��āA1����ꂽ�ȍ~�̐����̓�����́A����������܂��B
�����ŁA2�s�ڂ�2��ڂ�1����ꂽ�ꍇ���l���܂��B
2�s�ڂ�2������ʒu�́A1��ځA3��ځA4��ڂ�3�ʂ肠��܂����A����3�ʂ�ɂ��ẮA1�s�ڂ�1�̉���1��ڂƁA1�s�ڂ�3��4�̉���3��ڂ�4��ڂƂł́A�Ⴂ������܂��B1�͂��ł�2�s��2��ڂɓ����Ă��܂����A3��4�͂܂�2�s�ڂɓ����Ă��Ȃ�����ł��B�����ŁA2�s�ڂ�2������ʒu�ɂ��āA1��ڂɓ����ꍇ�ƁA3���4��ڂɓ����ꍇ�Ƃŕʂɍl���܂��B
(iii) �܂��A1�s�ڂ�1�̉���2�s��1��ڂ�2������ƁA1�s�ڂ�4�̉���2�s��4��ڂɂ�4�����邱�Ƃ��ł��Ȃ��̂ŁA2�s�ڂ͉��}�̂悤�ɁA����1�ʂ�Ɋm�肵�܂��B
3
�s�ڂ̓�����́A1��2�C3��4�̓���ւ��ɂ��A����4�ʂ�Ɍ����A����ɉ����āA4�s�ڂ��m�肵�܂��B�@����B(iv) 1�s�ڂ�3�C4�̉��A2�s�ڂ�3��ڂ�2������ꍇ�ƁA4��ڂ�2������ꍇ�Ƃ́A3��4�����ւ��čl����Ƃ��̑Ώ̐����A����������܂��B�����ŁA2��3��ڂɓ��ꂽ�ꍇ���l���܂��B1�s�ڂ�4�̉��ɂ�2�s��4��ڂɂ�4�͓���Ȃ��̂ŁA2�s�ڂ͂���1�ʂ�Ɋm�肵�A����ȍ~�A3�s�ڂɁA1��3��ڂɓ��邩4��ڂɓ��邩�ɂ���Ĉȉ���2�ʂ肠��܂��B�@����C
(iii)
�ŁA�B���A2�s��1��ڂ�2������Ƃ���4�ʂ�A�C���A2�s��3��ځA4��ڂ�2������Ƃ������ꂼ��2�ʂ�A���킹�āA2�s�ڂ�2�̓�����ɂ��A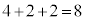 �ʂ肠��܂��B
�ʂ肠��܂��B
�A���A2�s�ڂ�1�̓������3�ʂ�A����3�ʂ�̊e1�ʂ�ɂ��Ĉȍ~��8�ʂ肠��̂ŁA2�s�ڈȍ~�A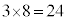 �ʂ肠��܂��B
�ʂ肠��܂��B
�@���A1�s�ڂ̐����̕��ѕ���24�ʂ肠��A���̊e1�ʂ�ɂ���2�s�ڈȍ~��24�ʂ肠��̂ŁA�����̓�����́A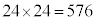 �ʂ� ......[��]
�ʂ� ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂��y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B