京都大学理系2020年数学入試問題

京都大学理系2020年数学入試問題

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。

[1]　a，bは実数で、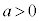

とする。zに関する方程式

･･･(＊)

は3つの相異なる解を持ち、それらは複素数平面上で、一辺の長さが

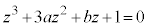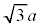の正三角形の頂点となっているとする。このとき、a，bと(＊)の3つの解を求めよ。
[解答へ]

[2]　pを正の整数とする。α，βはxに関する方程式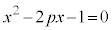

の2つの解で、

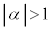であるとする。

(1) すべての正の整数nに対し、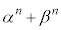

は整数であり、さらに偶数であることを証明せよ。

(2) 極限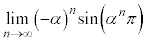

を求めよ。

[3]　kを正の実数とする。座標空間において、原点Oを中心とする半径1の球面上の4点A，B，C，Dが次の関係式を満たしている。

，

このとき、kの値を求めよ。ただし、座標空間の点X，Yに対して、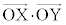

は、

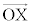と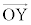

の内積を表す。
[解答へ]

[4]　正の整数aに対して、

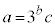(b，cは整数でcは3で割り切れない)

の形に書いたとき、

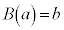と定める。例えば、

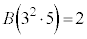である。

m，nは整数で、次の条件を満たすとする。

(i)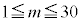

(ii)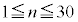

(iii) nは3で割り切れない。
このような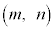

について

とするとき、

の最大値を求めよ。また、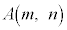

の最大値を与えるような

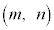をすべて求めよ。
[解答へ]

[5]　縦4個、横4個のマス目のそれぞれに1，2，3，4の数字を入れていく。このマス目の横の並びを行といい、縦の並びを列という。どの行にも、どの列にも同じ数字が1回しか現れない入れ方は何通りあるか求めよ。下図はこのような入れ方の1例である。

[6]　x，y，zを座標とする空間において、xz平面内の曲線

(

)

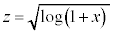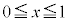をz軸のまわりに1回転させるとき、この曲線が通過した部分よりなる図形をSとする。このSをさらにx軸のまわりに1回転させるとき、Sが通過した部分よりなる立体をVとする。このとき、Vの体積を求めよ。
[解答へ]

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。

【広告】広告はここまでです。

苦学楽学塾 随時入会受付中！
理系大学受験ネット塾苦学楽学塾
(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。