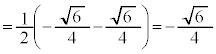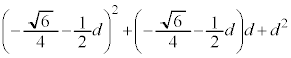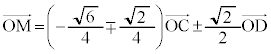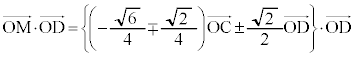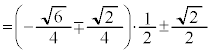���嗝�n���w'20�N�O��[3]
k�𐳂̎����Ƃ���B���W��Ԃɂ����āA���_O�𒆐S�Ƃ��锼�a1�̋��ʏ��4�_A�CB�CC�CD�����̊W�������Ă���B
���̂Ƃ��Ak�̒l�����߂�B�������A���W��Ԃ̓_X�CY�ɑ��āA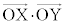 �́A
�́A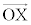 ��
��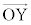 �̓��ς�\���B
�̓��ς�\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@4�_A�CB�CC�CD �́A���_�𒆐S�Ƃ��锼�a1�̋��ʏ�̓_�Ȃ̂ŁA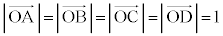 �C�܂��A
�C�܂��A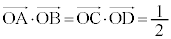 (��ԃx�N�g�����Q��)���A
(��ԃx�N�g�����Q��)���A
�܂�A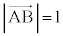 �C���l�ɁA
�C���l�ɁA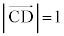
�]���āA��OAB�C��OCD�́A1�ӂ̒���1�̐��O�p�`�ł��B
�܂��A��蕶�̏������ŁA���̂܂�A��B�����ւ��Ă݂܂��B
�����ɕω��͂���܂���B�ł����A��蕶�̏�������C��D�����ւ���ƁA
�ƂȂ�A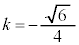 �ł��Ȃ�����������ω����Ă��܂��܂��B�܂�AA��B�ɂ��Ώ̐��������āAA��B�̐�������(2�_A�CB�̒��_��M�Ƃ���ƁAM��ʂ蒼��AB�ɐ����ȖʁA���̖ʂ�H�Ƃ��܂�)�ɂ��đΏ̂Ȉʒu�ɂ���܂��BC��D�ɂ͑Ώ̐��͂���܂���B
�ł��Ȃ�����������ω����Ă��܂��܂��B�܂�AA��B�ɂ��Ώ̐��������āAA��B�̐�������(2�_A�CB�̒��_��M�Ƃ���ƁAM��ʂ蒼��AB�ɐ����ȖʁA���̖ʂ�H�Ƃ��܂�)�ɂ��đΏ̂Ȉʒu�ɂ���܂��BC��D�ɂ͑Ώ̐��͂���܂���B
�_O�͐�������H��ɂ���܂��B�����łȂ���AA��B�����ւ���ƁA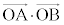 �̒l���ω����Ă��܂��܂��B
�̒l���ω����Ă��܂��܂��B
�_C�Ɠ_D���A�������R�ŁAA��B�����ւ����Ƃ��ɁA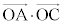 �C
�C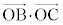 �C
�C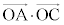 �C
�C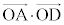 �̒l���ω����Ă��܂��̂ŁA��������H��ɂ���܂��B
�̒l���ω����Ă��܂��̂ŁA��������H��ɂ���܂��B
��Ԃ̖����ł������e�Ղɉ������߂̋Z�I�Ƃ��āA����f�ʏ�ŕ��ʂ̖��Ƃ��čl����A�Ƃ����Z�I������܂��B�{����A��������H��ŁA���ʃx�N�g���̖��Ƃ��čl���܂��B
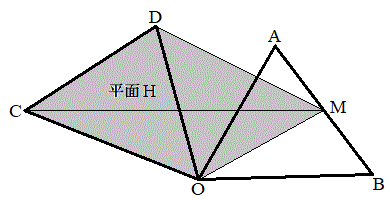
O�CM�CC�CD �͓��ꕽ��H��ɂ���A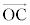 �C
�C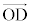 ���ꎟ�Ɨ��Ȃ̂ŁA
���ꎟ�Ɨ��Ȃ̂ŁA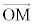 �́Ac�Cd�������Ƃ��āA
�́Ac�Cd�������Ƃ��āA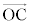 �C
�C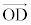 �̈ꎟ�����ŕ\����܂��B
�̈ꎟ�����ŕ\����܂��B
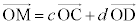 �@����@
�@����@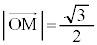 �ł��B
�ł��B
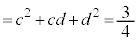 �@����A
�@����A
���A�@��p���āA
�� 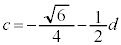 �@����B
�@����B
�A�ɑ�����āA
�� 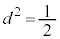 �C
�C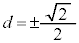
�B���A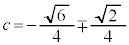
�@���A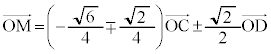
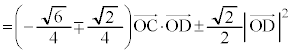
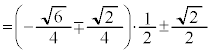
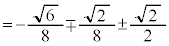
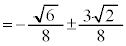 �@����C�@(�����܂ŁA��������)
�@����C�@(�����܂ŁA��������)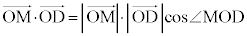 �̒l�́A��ԃx�N�g���ł����ʃx�N�g���ł��ς��Ȃ��̂ŁA��蕶�̏������A
�̒l�́A��ԃx�N�g���ł����ʃx�N�g���ł��ς��Ȃ��̂ŁA��蕶�̏������A
�C�ɂ������A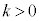 ���A
���A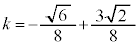 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B