���嗝�n���w'20�N�O��[1]
a�Cb�͎����ŁA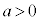 �Ƃ���Bz�Ɋւ��������
�Ƃ���Bz�Ɋւ��������
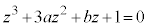 ���(��)
���(��)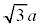 �̐��O�p�`�̒��_�ƂȂ��Ă���Ƃ���B���̂Ƃ��Aa�Cb��(��)��3�̉������߂�B
�̐��O�p�`�̒��_�ƂȂ��Ă���Ƃ���B���̂Ƃ��Aa�Cb��(��)��3�̉������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���f��������Ő��O�p�`�̒��_�ƂȂ��Ă���3���������̉��̍l�����͐F�X����܂��B�����ł́A1��3�捪��1�A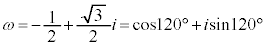 ���g���čl���Ă݂܂��B
���g���čl���Ă݂܂��B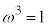 �C
�C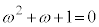 �ł��B
�ł��B
1�ӂ̒�����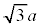 �̐��O�p�`�̊O�ډ~�̔��a��r�Ƃ���ƁA�����藝���A
�̐��O�p�`�̊O�ډ~�̔��a��r�Ƃ���ƁA�����藝���A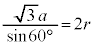 �@��
�@�� 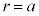
α��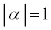 �ƂȂ镡�f���Ƃ���ƁA���_�𒆐S�Ƃ��锼�aa�̉~�����
�ƂȂ镡�f���Ƃ���ƁA���_�𒆐S�Ƃ��锼�aa�̉~�����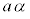 �C��������_�̎����
�C��������_�̎����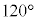 ��]����
��]����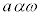 �C�����
�C�����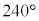 ��]����
��]����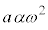 ��3�_���Ƃ�ƁA���O�p�`�ƂȂ�܂��B����ɁA����3�_�f�����ʏ��β�������s�ړ������A
��3�_���Ƃ�ƁA���O�p�`�ƂȂ�܂��B����ɁA����3�_�f�����ʏ��β�������s�ړ������A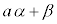 �C
�C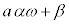 �C
�C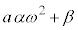 ���A(��)�̑��قȂ�3���ɂȂ��Ă���Ƃ��܂��B
���A(��)�̑��قȂ�3���ɂȂ��Ă���Ƃ��܂��B
3���������̉��ƌW���̊W���A
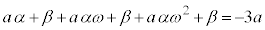 �@����@
�@����@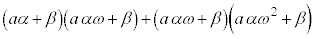
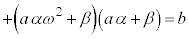 �@����A
�@����A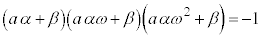 �@����B
�@����B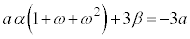 �@��
�@�� 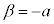 �@����C
�@����C
����āA(��)��3���́A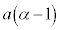 �C
�C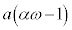 �C
�C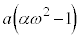 �ɂȂ�܂��B�@(����)
�ɂȂ�܂��B�@(����)
�A���A
�� 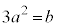 �@����D
�@����D
�B���A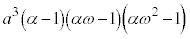
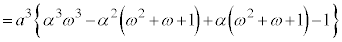
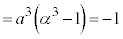 �@����E
�@����E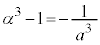 �@����F�@�͎����Ȃ̂ŁA
�@����F�@�͎����Ȃ̂ŁA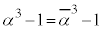 �C����āA
�C����āA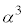 �������ł����A
�������ł����A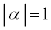 ���A
���A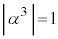 �@��
�@�� 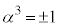
�F���A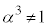 �Ȃ̂ŁA
�Ȃ̂ŁA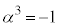 �C�F���A
�C�F���A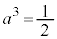 �Ca�͎����Ȃ̂ŁA
�Ca�͎����Ȃ̂ŁA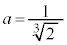 �C�D���A
�C�D���A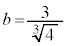
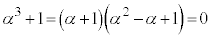 �@��
�@�� 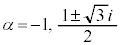
�E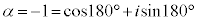 �̂Ƃ��A(����)��3���́A
�̂Ƃ��A(����)��3���́A 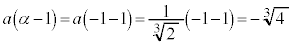 �@����G�C
�@����G�C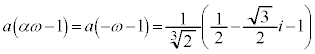
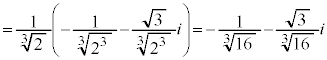 �@����H�C
�@����H�C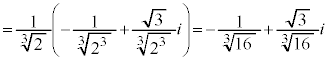 �@����I
�@����I�E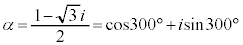 �̂Ƃ��A����α�́A
�̂Ƃ��A����α�́A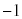 �����_�̎����
�����_�̎����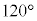 ��]�������_
��]�������_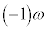 �Ȃ̂ŁA(����)��3���́A
�Ȃ̂ŁA(����)��3���́A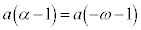 �͇H�Ɉ�v���A
�͇H�Ɉ�v���A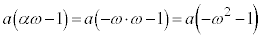 �͇I�Ɉ�v���A
�͇I�Ɉ�v���A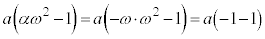 �͇G�Ɉ�v���܂��B
�͇G�Ɉ�v���܂��B �E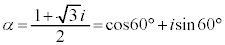 �̂Ƃ��A����α�́A
�̂Ƃ��A����α�́A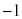 �����_�̎����
�����_�̎����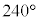 ��]�������_
��]�������_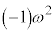 �Ȃ̂ŁA(����)��3���́A
�Ȃ̂ŁA(����)��3���́A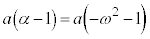 �͇I�Ɉ�v���A
�͇I�Ɉ�v���A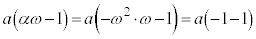 �͇G�Ɉ�v���A
�͇G�Ɉ�v���A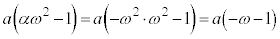 �͇H�Ɉ�v���܂��B
�͇H�Ɉ�v���܂��B �ȏ���A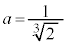 �C
�C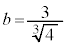 �C(��)��3���́A
�C(��)��3���́A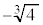 �C
�C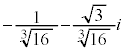 �C
�C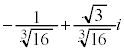 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 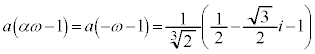
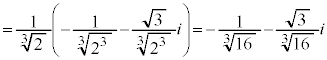 �@����H�C
�@����H�C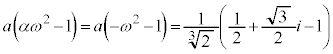
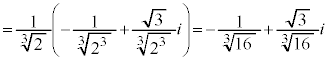 �@����I
�@����I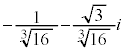 �C
�C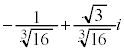 ......[��]
......[��]