京大理系数学'21年前期[5]
xy平面において、2点B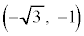 ,C
,C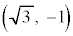 に対し、点Aは次の条件(*)を満たすとする。
に対し、点Aは次の条件(*)を満たすとする。
(*) 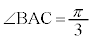 かつ点Aのy座標は正。
かつ点Aのy座標は正。
次の各問に答えよ。
(1) △ABCの外心の座標を求めよ。
(2) 点Aが条件(*)を満たしながら動くとき、△ABCの垂心の軌跡を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 京大は平面図形の問題が多いので、平面図形として解いてみます。なお、三角形の五心を参照してください。
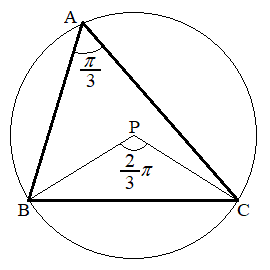 (1) △ABCの外心Pは、△ABCの外接円の中心なので、中心角
(1) △ABCの外心Pは、△ABCの外接円の中心なので、中心角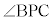 は円周角
は円周角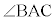 の2倍で、
の2倍で、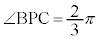
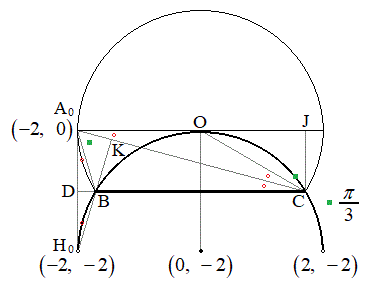
 (2) Bから対辺CAに垂線BKを下ろし、Cから対辺ABに垂線CLを下ろし、Aから対辺BCに垂線AMを下ろし、直線BKと直線CLと直線AMの交点をHとすると、Hは△ABCの垂心です。
(2) Bから対辺CAに垂線BKを下ろし、Cから対辺ABに垂線CLを下ろし、Aから対辺BCに垂線AMを下ろし、直線BKと直線CLと直線AMの交点をHとすると、Hは△ABCの垂心です。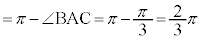 (
(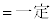 )
)よって、円周角の定理の逆より、Hの軌跡は円弧になります。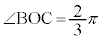 なので、Hは原点Oにも来ます。
なので、Hは原点Oにも来ます。 を円弧とする円は、△BOCの外接円です。外接円の半径Rは、正弦定理:
を円弧とする円は、△BOCの外接円です。外接円の半径Rは、正弦定理: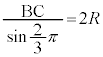 より
より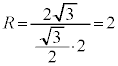 、円の対称性より、この円の中心は辺BCの垂直二等分線(y軸)上にあり、原点Oとの距離が2となる点
、円の対称性より、この円の中心は辺BCの垂直二等分線(y軸)上にあり、原点Oとの距離が2となる点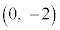 です。
です。
 ところで、Aが領域
ところで、Aが領域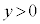 の端点
の端点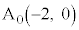 に来るとき、
に来るとき、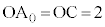 より
より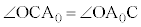 ,また、
,また、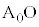 //BCより
//BCより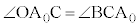 (錯角)
(錯角)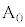 から直線BCに垂線
から直線BCに垂線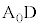 を下ろし、Bから直線
を下ろし、Bから直線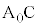 に垂線BKを下ろし、直線
に垂線BKを下ろし、直線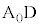 と直線BKとの交点(△
と直線BKとの交点(△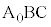 の垂心)を
の垂心)を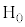 とします。
とします。
またCから直線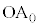 (x軸)に垂線CJを下ろすと、
(x軸)に垂線CJを下ろすと、 よって、△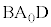 ≡△
≡△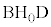 (BD共通で、直角三角形の1辺と2角が等しい) ∴
(BD共通で、直角三角形の1辺と2角が等しい) ∴ 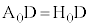 これより、
これより、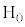 の座標は
の座標は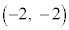
全く同様に、Aが領域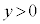 の端点
の端点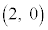 に来るとき、垂心Hは
に来るとき、垂心Hは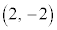 に来ます。垂心Hの軌跡となる円弧は、
に来ます。垂心Hの軌跡となる円弧は、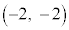 ,
,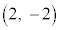 を結ぶ直線
を結ぶ直線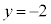 よりも上側にある円周の部分です。
よりも上側にある円周の部分です。
以上より、垂心Hの軌跡は、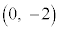 を中心とする半径2の円の
を中心とする半径2の円の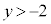 の部分 ......[答]
の部分 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 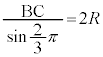 より
より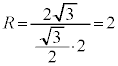 、円の対称性より、この円の中心は辺BCの垂直二等分線(y軸)上にあり、原点Oとの距離が2となる点
、円の対称性より、この円の中心は辺BCの垂直二等分線(y軸)上にあり、原点Oとの距離が2となる点