京都大学理系2021年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 次の各問に答えよ。
問1 xyz空間の3点A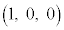 ,B
,B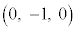 ,C
,C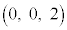 を通る平面αに関して点P
を通る平面αに関して点P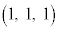 と対称な点Qの座標を求めよ。ただし、点Qが平面αに関してPと対称であるとは、線分PQの中点Mが平面α上にあり、直線PMがPから平面αに下ろした垂線となることである。
と対称な点Qの座標を求めよ。ただし、点Qが平面αに関してPと対称であるとは、線分PQの中点Mが平面α上にあり、直線PMがPから平面αに下ろした垂線となることである。 問2 赤玉、白玉、青玉、黄玉が1個ずつ入った袋がある。よくかきまぜた後に袋から玉を1個取り出し、その玉の色を記録してから袋に戻す。この試行を繰り返すとき、n回目の試行で初めて赤玉が取り出されて4種類全ての色が記録済みとなる確率を求めよ。ただしnは4以上の整数とする。
[解答へ]
[2] 曲線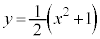 上の点Pにおける接線はx軸と交わるとし、その交点をQとおく。線分PQの長さをLとするとき、Lが取りうる値の最小値を求めよ。
上の点Pにおける接線はx軸と交わるとし、その交点をQとおく。線分PQの長さをLとするとき、Lが取りうる値の最小値を求めよ。
[解答へ]
[3] 無限級数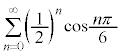 の和を求めよ。
の和を求めよ。
[解答へ]
[4] 曲線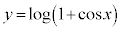 の
の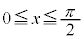 の部分の長さを求めよ。
の部分の長さを求めよ。
[解答へ]
[5] xy平面において、2点B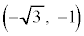 ,C
,C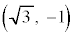 に対し、点Aは次の条件(*)を満たすとする。
に対し、点Aは次の条件(*)を満たすとする。
(*) 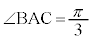 かつ点Aのy座標は正。
かつ点Aのy座標は正。
次の各問に答えよ。
(1) △ABCの外心の座標を求めよ。
(2) 点Aが条件(*)を満たしながら動くとき、△ABCの垂心の軌跡を求めよ。
[解答へ]
[6] 次の各問に答えよ。
問1 nを2以上の整数とする。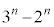 が素数ならばnも素数であることを示せ。
が素数ならばnも素数であることを示せ。 問2 aを1より大きい定数とする。微分可能な関数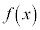 が
が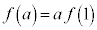 を満たすとき、曲線
を満たすとき、曲線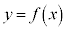 の接線で原点
の接線で原点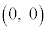 を通るものが存在することを示せ。
を通るものが存在することを示せ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 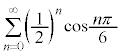 の和を求めよ。
の和を求めよ。