���嗝�n���w'21�N�O��[6]
���̊e��ɓ�����B
��1�@n��2�ȏ�̐����Ƃ���B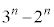 ���f���Ȃ��n���f���ł��邱�Ƃ������B
���f���Ȃ��n���f���ł��邱�Ƃ������B ��2�@a��1���傫���萔�Ƃ���B�����\�Ȋ�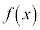 ��
��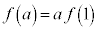 �����Ƃ��A�Ȑ�
�����Ƃ��A�Ȑ�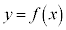 �̐ڐ��Ō��_
�̐ڐ��Ō��_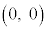 ��ʂ���̂����݂��邱�Ƃ������B
��ʂ���̂����݂��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��2�̕��́A��ӂ��킩��Â炢�����m��܂���B
��1�@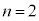 �̂Ƃ��A
�̂Ƃ��A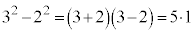 ���f���ł��B�m����
���f���ł��B�m����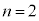 ���f���ł��B
���f���ł��B
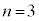 �̂Ƃ��A
�̂Ƃ��A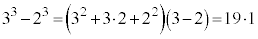 �͑f���ł��B�m����
�͑f���ł��B�m����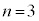 ���f���ł��B
���f���ł��B
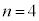 �̂Ƃ��A
�̂Ƃ��A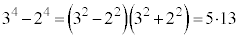 �́A2�ȏ�̎��R���̐ςƂȂ�f���ł͂Ȃ��A
�́A2�ȏ�̎��R���̐ςƂȂ�f���ł͂Ȃ��A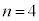 ���f���ł͂Ȃ��A�Ƃ������ƂɂȂ�܂��B�ł����A
���f���ł͂Ȃ��A�Ƃ������ƂɂȂ�܂��B�ł����A�Ƃ����Ƃ��ɁA�E�ӂ�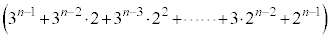 ���f�����ǂ����f����̂͗e�Ղł͂Ȃ��A�Ƃ������ƂŁA�f�����ǂ����������₷��n�̕�����l���Ă��������̂ł��B�����ŁA��蕶�̂܂܍l���Ă����̂ł͂Ȃ��A��蕶�������������ƂɂȂ�܂��B�{��̑�́A
���f�����ǂ����f����̂͗e�Ղł͂Ȃ��A�Ƃ������ƂŁA�f�����ǂ����������₷��n�̕�����l���Ă��������̂ł��B�����ŁA��蕶�̂܂܍l���Ă����̂ł͂Ȃ��A��蕶�������������ƂɂȂ�܂��B�{��̑�́A �u2�ȏ�̐���n���f���łȂ���A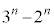 �͑f���łȂ��v�@���(��)
�͑f���łȂ��v�@���(��) 2�ȏ�̐���n���f���łȂ��Ƃ��A2��2�ȏ�̎��R��k�Cm�̐ςƂ��āA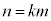 �Ə����܂��B���̂Ƃ��A
�Ə����܂��B���̂Ƃ��A 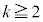 �Ȃ̂ŁA
�Ȃ̂ŁA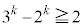 �C
�C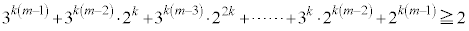 ���A�E�ӂ�2��2�ȏ�̎��R���̐ς̌`�����Ă��āA�f���ł͂���܂���B����āA(��)�������܂����B(��)�̑�ł���A�u
���A�E�ӂ�2��2�ȏ�̎��R���̐ς̌`�����Ă��āA�f���ł͂���܂���B����āA(��)�������܂����B(��)�̑�ł���A�u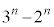 ���f���Ȃ��n���f���ł���v�����藧���܂��B
���f���Ȃ��n���f���ł���v�����藧���܂��B
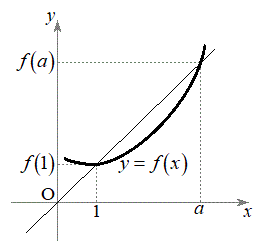 ��2�@�܂��Aa�͒萔�ł����ĕϐ��ł͂Ȃ����Ƃɒ��ӂ��܂��B
��2�@�܂��Aa�͒萔�ł����ĕϐ��ł͂Ȃ����Ƃɒ��ӂ��܂��B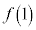 ��
��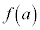 ���o�Ă���̂ŁA�Ȑ�
���o�Ă���̂ŁA�Ȑ�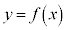 ���2�_
���2�_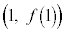 �C
�C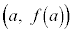 ��ʂ钼�����l����ƁA���̌X���́A
��ʂ钼�����l����ƁA���̌X���́A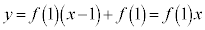 �@����@
�@����@�ƂȂ�A�����@�����_��ʂ邱�Ƃ��킩��܂��B���ꂪ�A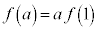 �̈Ӗ��ł��B
�̈Ӗ��ł��B
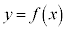 ��
��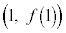 �ɂ������ڐ��́A
�ɂ������ڐ��́A 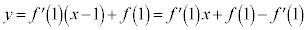 �@����A
�@����A�ƂȂ�܂����A�A��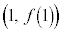 �ɂ�����́A�ڐ��̌X��
�ɂ�����́A�ڐ��̌X��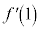 �Ɋւ��Ĉȉ���3�ʂ肠��܂��B
�Ɋւ��Ĉȉ���3�ʂ肠��܂��B (i) �ڐ��A�̌X���������@�̌X�������������A�܂�A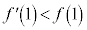 �@����B
�@����B (ii) �ڐ��A�̌X���������@�̌X���Ɠ������A�܂�A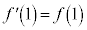
(iii) �ڐ��A�̌X���������@�̌X�������傫���A�܂�A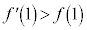 �@����C
�@����C ��L��(ii)�̏ꍇ�A�A��y�ؕЁF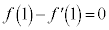 �ƂȂ�̂ŁA�ڐ��A(�����@�Ɉ�v)�͌��_
�ƂȂ�̂ŁA�ڐ��A(�����@�Ɉ�v)�͌��_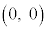 ��ʂ�܂��B
��ʂ�܂��B 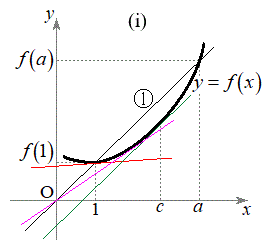 (i)�̏ꍇ�A���Ȃ��Ƃ�
(i)�̏ꍇ�A���Ȃ��Ƃ�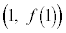 �̋ߖT(�����߂�)��
�̋ߖT(�����߂�)��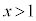 �̕����ɂ����āA�Ȑ�
�̕����ɂ����āA�Ȑ�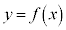 �͒����@�̉����ɗ��܂��B���̂��ƁA�Ȑ�
�͒����@�̉����ɗ��܂��B���̂��ƁA�Ȑ�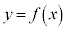 ��
��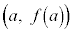 ��ʉ߂���̂ŁA�����@�ƕ��s��
��ʉ߂���̂ŁA�����@�ƕ��s��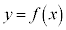 �̐ڐ�(�E�}�ΐ�)�ł����āA�����@�̉����ɗ�����̂����݂��܂��B���ϒl�̒藝���g���ď����ƁA
�̐ڐ�(�E�}�ΐ�)�ł����āA�����@�̉����ɗ�����̂����݂��܂��B���ϒl�̒藝���g���ď����ƁA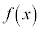 �͔����\�Ȋ��Ȃ̂ŁA
�͔����\�Ȋ��Ȃ̂ŁA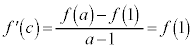 �C
�C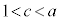
����c�����݂��܂�(�������݂���ꍇ�ɂ�1�ɍł��߂����̂�I�т܂�)�B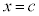 �ɂ�����ڐ�(�E�}�ΐ�)�F
�ɂ�����ڐ�(�E�}�ΐ�)�F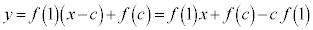 �́A�����@�ƕ��s�ł����Ă������ɂ���̂ŁAy�ؕЁF
�́A�����@�ƕ��s�ł����Ă������ɂ���̂ŁAy�ؕЁF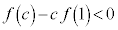 �ł��B
�ł��B
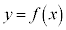 ��
��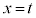 �ɂ�����ڐ��F
�ɂ�����ڐ��F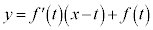 ��y�ؕЂ�
��y�ؕЂ�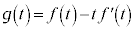 �Ƃ����ƁA
�Ƃ����ƁA 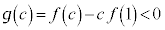 �C�B���A
�C�B���A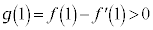
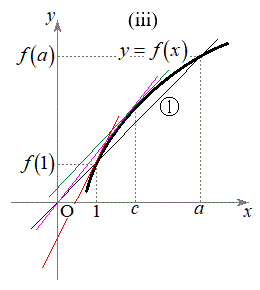 (iii)�̏ꍇ��(i)�Ƃقړ��l�ł����A���Ȃ��Ƃ�
(iii)�̏ꍇ��(i)�Ƃقړ��l�ł����A���Ȃ��Ƃ�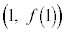 �̋ߖT��
�̋ߖT��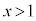 �̕����ɂ����āA�Ȑ�
�̕����ɂ����āA�Ȑ�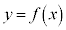 �͒����@�̏㑤�ɗ��܂��B���ϒl�̒藝���A
�͒����@�̏㑤�ɗ��܂��B���ϒl�̒藝���A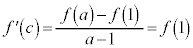 �C
�C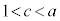
����c�����݂��܂��Bc���������݂���Ƃ��ɂ́A1�ɍł��߂����̂�I�ׂA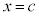 �ɂ�����ڐ�(�E�}�ΐ�)�F
�ɂ�����ڐ�(�E�}�ΐ�)�F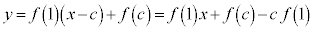 �́A�����@�ƕ��s�ł����Ă��㑤�ɗ���̂ŁA�ڐ���y�ؕЁF
�́A�����@�ƕ��s�ł����Ă��㑤�ɗ���̂ŁA�ڐ���y�ؕЁF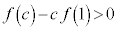 �ł��B�ڐ���y�ؕЂ�
�ł��B�ڐ���y�ؕЂ�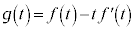 �Ƃ����ƁA
�Ƃ����ƁA 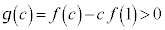 �C�C���A
�C�C���A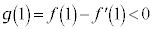
�ʉ��D��L�́A�}�`�I�ɍl�@��i�߂܂������A��L�̐}�ł킩��ʂ�A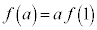 �̂Ƃ��A�Ȑ�
�̂Ƃ��A�Ȑ�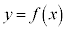 �̐ڐ������_��ʉ߂���((i)�C(iii)�̐}�̃s���N�F�̒���)�̂́A�Ȑ���̓_�ƌ��_�����Ԓ����̌X�����ɒl���Ƃ�Ƃ��Ȃ̂ŁA�Ȑ���̓_
�̐ڐ������_��ʉ߂���((i)�C(iii)�̐}�̃s���N�F�̒���)�̂́A�Ȑ���̓_�ƌ��_�����Ԓ����̌X�����ɒl���Ƃ�Ƃ��Ȃ̂ŁA�Ȑ���̓_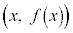 �ƌ��_�����Ԓ����̌X����l�Ƃ����
�ƌ��_�����Ԓ����̌X����l�Ƃ����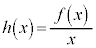 ���g���Ĉȉ��̂悤�ɍl���邱�Ƃ��ł��܂�(������ɉƂɖ߂��Ă���Ȃ�l�����邩���m��܂��A������Ŏv�����邩�ǂ����͋^��ł�)�B
���g���Ĉȉ��̂悤�ɍl���邱�Ƃ��ł��܂�(������ɉƂɖ߂��Ă���Ȃ�l�����邩���m��܂��A������Ŏv�����邩�ǂ����͋^��ł�)�B 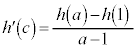 �@����D�C
�@����D�C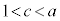
�ƂȂ�c�����݂��܂��B�Ƃ���ŁA
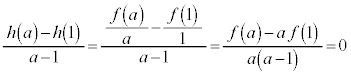 �@����E
�@����E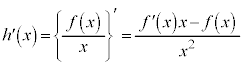
�D�C�E���A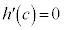 �Ȃ̂ŁA
�Ȃ̂ŁA 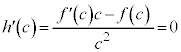 �@��
�@�� 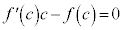
�Ȑ�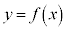 ��
��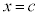 �ɂ�����ڐ��́A
�ɂ�����ڐ��́A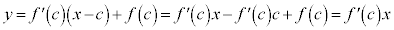
����́A���_��ʂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 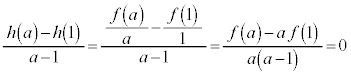 �@����E
�@����E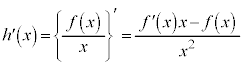
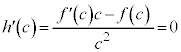 �@��
�@��