���嗝�n���w'21�N�O��[1]
���̊e��ɓ�����B
��1�@xyz��Ԃ�3�_A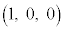 �CB
�CB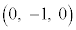 �CC
�CC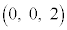 ��ʂ镽��α�Ɋւ��ē_P
��ʂ镽��α�Ɋւ��ē_P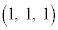 �ƑΏ̂ȓ_Q�̍��W�����߂�B�������A�_Q������α�Ɋւ���P�ƑΏ̂ł���Ƃ́A����PQ�̒��_M������α��ɂ���A����PM��P���畽��α�ɉ��낵�������ƂȂ邱�Ƃł���B
�ƑΏ̂ȓ_Q�̍��W�����߂�B�������A�_Q������α�Ɋւ���P�ƑΏ̂ł���Ƃ́A����PQ�̒��_M������α��ɂ���A����PM��P���畽��α�ɉ��낵�������ƂȂ邱�Ƃł���B ��2�@�ԋʁA���ʁA�ʁA���ʂ�1���������܂�����B�悭�����܂�����ɑ܂���ʂ�1���o���A���̋ʂ̐F���L�^���Ă���܂ɖ߂��B���̎��s���J��Ԃ��Ƃ��An��ڂ̎��s�ŏ��߂Đԋʂ����o�����4��ޑS�Ă̐F���L�^�ς݂ƂȂ�m�������߂�B������n��4�ȏ�̐����Ƃ���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�E�H�[�~���O�E�A�b�v���2��ł��B
��1�@����α���������́Ax�ؕЂ�1�Cy�ؕЂ�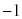 �Cz�ؕЂ�2�ł��邱�Ƃ���A
�Cz�ؕЂ�2�ł��邱�Ƃ���A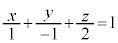
�܂�A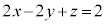 �@����@
�@����@
������A����α���@���x�N�g���́A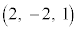 �C
�C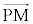 �͕���α�Ɛ����Ŗ@���x�N�g���ƕ��s�B����āAt �������Ƃ��āA
�͕���α�Ɛ����Ŗ@���x�N�g���ƕ��s�B����āAt �������Ƃ��āA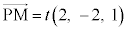 �Ƃ����܂��B
�Ƃ����܂��B M�͕���α��̓_�Ȃ̂ŁA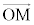 �̊e�����A�܂�M�̍��W���@�ɑ�����āA
�̊e�����A�܂�M�̍��W���@�ɑ�����āA ����āAQ�̍��W�́A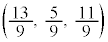 ......[��]
......[��] �ʉ��D��L�ł����ʂ̕������Ɋւ���m����p���ĉ����܂������A���ʂ̕��������g��Ȃ��̂ł���A�ȉ��̂悤�ɂȂ�܂�(��ԃx�N�g�����Q��)�B ����α�̖@���x�N�g���A�܂�A����α�ɐ����ȃx�N�g��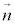 �́A
�́A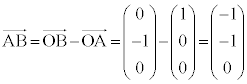 �C
�C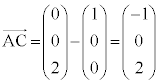 �̑o���ɐ����ȃx�N�g���Ƃ��āA
�̑o���ɐ����ȃx�N�g���Ƃ��āA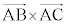 (�O��)���A�ȉ��̂悤�Ɍv�Z����ƁA
(�O��)���A�ȉ��̂悤�Ɍv�Z����ƁA 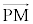 //
// 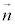 ���Ak�������Ƃ��āA
���Ak�������Ƃ��āA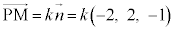 �C
�C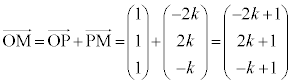 �C
�C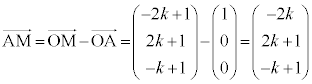 �́A����α��̃x�N�g���Ȃ̂ŁA
�́A����α��̃x�N�g���Ȃ̂ŁA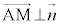 ���A
���A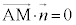 (�������Q��)�C����āA
(�������Q��)�C����āA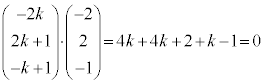 �@��
�@�� 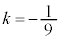
������A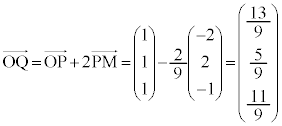 �ƂȂ�܂��B
�ƂȂ�܂��B
��2�@ n��ڂ̎��s�ŏ��߂Đԋʂ����o�����4��ޑS�Ă̐F���L�^�ς݂ƂȂ�A�Ƃ������Ƃ́A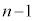 ��ڂ܂ł́A�ԋʂ��o���A���A���ʁA�ʁA���ʂ����Ȃ��Ƃ�1��͏o�āAn��ڂŐԋʂ��o��A�Ƃ������Ƃł��B�u���Ȃ��Ƃ��v�Ƃ����L�[���[�h���o�Ă���̂��]�����̕��A�܂�A
��ڂ܂ł́A�ԋʂ��o���A���A���ʁA�ʁA���ʂ����Ȃ��Ƃ�1��͏o�āAn��ڂŐԋʂ��o��A�Ƃ������Ƃł��B�u���Ȃ��Ƃ��v�Ƃ����L�[���[�h���o�Ă���̂��]�����̕��A�܂�A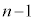 ��ڂ܂łɁA���ʂ�1����o�Ȃ����A�܂��́A�ʂ�1����o�Ȃ����A�܂��́A���ʂ�1����o�Ȃ��ꍇ���l���܂��B
��ڂ܂łɁA���ʂ�1����o�Ȃ����A�܂��́A�ʂ�1����o�Ȃ����A�܂��́A���ʂ�1����o�Ȃ��ꍇ���l���܂��B 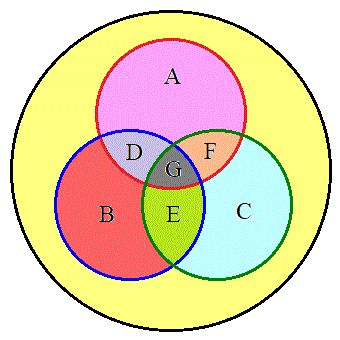 1��̎��s�Őԋʂ��o�Ȃ��m����
1��̎��s�Őԋʂ��o�Ȃ��m����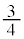 �Ȃ̂ŁA
�Ȃ̂ŁA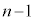 ��ڂ܂ŁA�ԋʂ�1����o�Ȃ�(�E�}�ō����~�̓���)�m���́A
��ڂ܂ŁA�ԋʂ�1����o�Ȃ�(�E�}�ō����~�̓���)�m���́A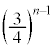 �@����@
�@����@���D�ȉ��A�킩��ɂ����̂ŁA�E�}�����Ȃ���l���Ă��������B�E�}�ŁA�Ԃ��~�̓����́A�ԋʂɉ����Đʂ�1����o�Ȃ��ꍇ�A���~�̓����́A�ԋʂɉ����ĉ��ʂ�1����o�Ȃ��ꍇ�A�ΐF�̉~�̓����́A�ԋʂɉ����Ĕ��ʂ�1����o�Ȃ��ꍇ�A3�~���d�Ȃ��Ă���D�F�̈�G�́A�ԋʂ��ʂ����ʂ����ʂ�1����o�Ȃ��ꍇ�ł����A����͂��蓾�Ȃ��̂ŋ�W���B
�@�̂����ŁA���ʂ���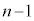 ��o��(�E�}�Ŕ����̗̈�D)�m����
��o��(�E�}�Ŕ����̗̈�D)�m����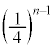 �@����A�C�ʂ���
�@����A�C�ʂ���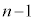 ��o��(�E�}�ʼn��ΐF�̗̈�E)�A���ʂ���
��o��(�E�}�ʼn��ΐF�̗̈�E)�A���ʂ���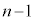 ��o��(�E�}�Ş�F�̗̈�F)�̂�������
��o��(�E�}�Ş�F�̗̈�F)�̂�������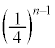 �ł��B
�ł��B
�܂��A�@�̂����ŁA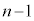 ��ڂ܂ŁA�ʂ��邢�͉��ʂ�����
��ڂ܂ŁA�ʂ��邢�͉��ʂ�����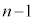 ��o��(�܂�A���ʂƐԋʂ�1����o�Ȃ��A�E�}�ŗ̈�C�Ɨ̈�E�Ɨ̈�F�����킹���ΐF�̉~�̓���)�m���́A
��o��(�܂�A���ʂƐԋʂ�1����o�Ȃ��A�E�}�ŗ̈�C�Ɨ̈�E�Ɨ̈�F�����킹���ΐF�̉~�̓���)�m���́A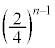 �@����B
�@����B
�A���A���̒��A�܂�A�ʂ��邢�͉��ʂ�����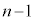 ��o�邤���ɂ́A�ʂ���
��o�邤���ɂ́A�ʂ���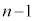 ��o��(���ʂ�1����o�Ȃ��A�E�}�̗̈�E)�ꍇ�A�ƁA���ʂ���
��o��(���ʂ�1����o�Ȃ��A�E�}�̗̈�E)�ꍇ�A�ƁA���ʂ���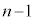 ��o��(�ʂ�1����o�Ȃ��A�E�}�̗̈�F)�ꍇ���܂ނ̂ŁA�d��������āA���ʂƐԋʂ�1����o���ɁA�ʂ����Ȃ��Ƃ�1��o�ĉ��ʂ����Ȃ��Ƃ�1��o��(�E�}�̐��F�̗̈�C)�m���́A�B�|�A�~2�Ƃ���(�ΐF�̉~�̓������物�ΐFE�ƞ�FF������)�A
��o��(�ʂ�1����o�Ȃ��A�E�}�̗̈�F)�ꍇ���܂ނ̂ŁA�d��������āA���ʂƐԋʂ�1����o���ɁA�ʂ����Ȃ��Ƃ�1��o�ĉ��ʂ����Ȃ��Ƃ�1��o��(�E�}�̐��F�̗̈�C)�m���́A�B�|�A�~2�Ƃ���(�ΐF�̉~�̓������物�ΐFE�ƞ�FF������)�A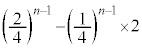 �@����C
�@����C
�ʂƐԋʂ�1����o���ɁA���ʂ����Ȃ��Ƃ�1��o�Ĕ��ʂ����Ȃ��Ƃ�1��o��(�E�}�̃s���N�F�̗̈�A)�m���������ł��B
���ʂƐԋʂ�1����o���ɁA�ʂ����Ȃ��Ƃ�1��o�Ĕ��ʂ����Ȃ��Ƃ�1��o��(�E�}�̒W�ԐF�̗̈�B)�m���������ł��B
�ȏ���A ��ڂ܂łɁA���ʂ�1����o�Ȃ����A�܂��́A�ʂ�1����o�Ȃ����A�܂��́A���ʂ�1����o�Ȃ�(�E�}�ŐԂ��~�����A���~�����A�̉~���������킹���̈�)�m���́A�A�~3�{�C�~3�Ƃ���(�̈�A�CB�CC�CD�CE�CF�����킹��)�A
��ڂ܂łɁA���ʂ�1����o�Ȃ����A�܂��́A�ʂ�1����o�Ȃ����A�܂��́A���ʂ�1����o�Ȃ�(�E�}�ŐԂ��~�����A���~�����A�̉~���������킹���̈�)�m���́A�A�~3�{�C�~3�Ƃ���(�̈�A�CB�CC�CD�CE�CF�����킹��)�A 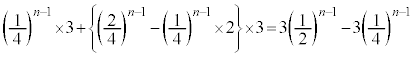 �@����D
�@����D ��ڂ܂ŁA�ԋʂ��o���A���A���ʁA�ʁA���ʂ����Ȃ��Ƃ�1��͏o��(�E�}�ʼn��F�̗̈�)�m���͇@�|�D�ŁA
��ڂ܂ŁA�ԋʂ��o���A���A���ʁA�ʁA���ʂ����Ȃ��Ƃ�1��͏o��(�E�}�ʼn��F�̗̈�)�m���͇@�|�D�ŁAn��ڂɐԋʂ��o��m����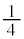 �Ȃ̂ŁAn��ڂ̎��s�ŏ��߂Đԋʂ����o�����4��ޑS�Ă̐F���L�^�ς݂ƂȂ�m���́A
�Ȃ̂ŁAn��ڂ̎��s�ŏ��߂Đԋʂ����o�����4��ޑS�Ă̐F���L�^�ς݂ƂȂ�m���́A 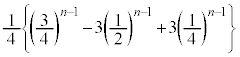 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 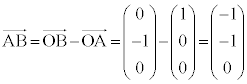 �C
�C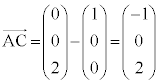 �̑o���ɐ����ȃx�N�g���Ƃ��āA
�̑o���ɐ����ȃx�N�g���Ƃ��āA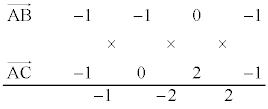
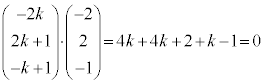 �@��
�@�� 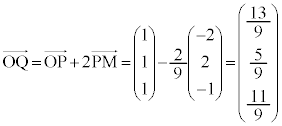 �ƂȂ�܂��B
�ƂȂ�܂��B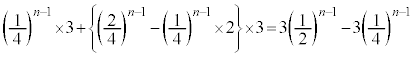 �@����D
�@����D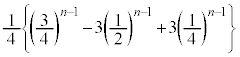 ......[��]
......[��]