京大理系数学'22年前期[3]
nを自然数とする。3つの整数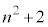 ,
,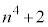 ,
,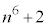 の最大公約数
の最大公約数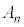 を求めよ。
を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 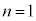 のとき
のとき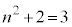 ,
,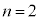 のとき
のとき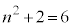 ,
,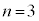 のとき
のとき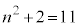 ,
,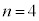 のとき
のとき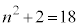 ,
,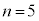 のとき
のとき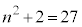 ,
,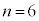 のとき
のとき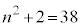 となるので、規則性があることに見当がつくと思います。
となるので、規則性があることに見当がつくと思います。
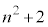 が約数mを持つとすると、kを自然数として、
が約数mを持つとすると、kを自然数として、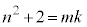 と表せます。このとき、
と表せます。このとき、
よって、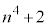 も約数mをもつとすると、mは6の約数です。
も約数mをもつとすると、mは6の約数です。
よって、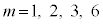 のいずれかです。
のいずれかです。
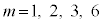 のいずれかのとき、
のいずれかのとき、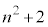 ,
,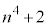 ともmの倍数ですが、
ともmの倍数ですが、
より、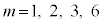 のいずれかであれば、
のいずれかであれば、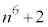 もmの倍数です。つまり、
もmの倍数です。つまり、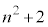 ,
,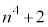 ,
,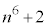 の最大公約数は、1,2,3,6のいずれかに限られます。
の最大公約数は、1,2,3,6のいずれかに限られます。
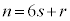 (s:整数、
(s:整数、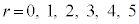 )とおくと、
)とおくと、
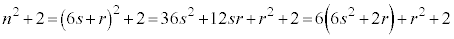
これは、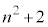 が6の倍数+(
が6の倍数+(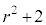 )という形に表せる(mod記号を使うと、
)という形に表せる(mod記号を使うと、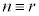 (mod. 6)のとき
(mod. 6)のとき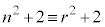 (mod. 6),剰余類を参照)であることを意味しています。
(mod. 6),剰余類を参照)であることを意味しています。
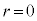 のとき、
のとき、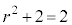 なので、
なので、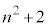 は2の倍数ですが3,6の倍数にはなりません。このとき、
は2の倍数ですが3,6の倍数にはなりません。このとき、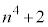 (
(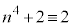 (mod. 6)),
(mod. 6)),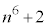 (
(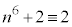 (mod. 6))も2の倍数で、
(mod. 6))も2の倍数で、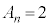
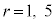 のとき、
のとき、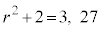 なので、
なので、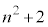 は奇数であって3の倍数ですが6の倍数にはなりません。このとき、
は奇数であって3の倍数ですが6の倍数にはなりません。このとき、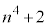 (
(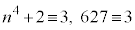 (mod. 6)),
(mod. 6)),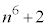 (
(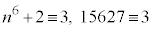 (mod. 6))も3の倍数で、
(mod. 6))も3の倍数で、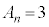
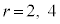 のとき、
のとき、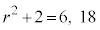 なので、
なので、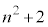 は6の倍数です。
は6の倍数です。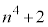 (
(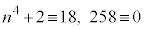 (mod. 6)),
(mod. 6)),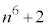 (
(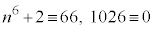 (mod. 6))も6の倍数で、
(mod. 6))も6の倍数で、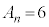
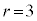 のとき、
のとき、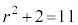 なので、
なので、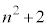 は奇数であって、3の倍数にはなりません。このときは、
は奇数であって、3の倍数にはなりません。このときは、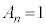
以上より、nが6で割り切れるとき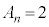 ,nが6で割って余りが1か5のとき
,nが6で割って余りが1か5のとき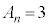 ,nが6で割って余りが2か4のとき
,nが6で割って余りが2か4のとき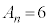 ,nが6で割って余りが3のとき
,nが6で割って余りが3のとき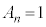 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。