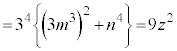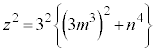���嗝�n���w'25�N�O��[2]
���̐���x�Cy�Cz��p����
�ƕ\����鐳�̐���N�̍ŏ��l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�J�������s�����A���N�̐���N�ɂ��āA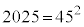 �ł��邱�Ƃ�F�����Ă��Ď��ɂƂ��Ă͈Ֆ₾���������m��܂���(
�ł��邱�Ƃ�F�����Ă��Ď��ɂƂ��Ă͈Ֆ₾���������m��܂���(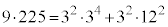 �ł�)�B�����ł́A��]����p���Đ��U�@�ł���Ă݂܂��B
�ł�)�B�����ł́A��]����p���Đ��U�@�ł���Ă݂܂��B
�܂��AN��9�̔{���Ȃ̂ŁA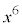 �C
�C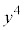 ��3�̔{�����ǂ����A���̑O�ɁA
��3�̔{�����ǂ����A���̑O�ɁA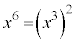 �C
�C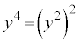 �Ȃ̂ŁA
�Ȃ̂ŁA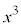 �C
�C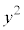 ��3�̔{�����ǂ����ׂĂ݂܂��B
��3�̔{�����ǂ����ׂĂ݂܂��B
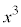 �C
�C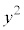 ���Ƃ���3�̔{���ł���A
���Ƃ���3�̔{���ł���A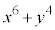 ��9�̔{���ɂȂ�܂��B
��9�̔{���ɂȂ�܂��B
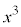 �C
�C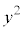 ���Ƃ���3�̔{���łȂ��A�Ƃ���ƁA�ȉ���4�̏ꍇ������܂��B�ȉ��ł́Ak�Cl��0�ȏ�������Ƃ��܂��B
���Ƃ���3�̔{���łȂ��A�Ƃ���ƁA�ȉ���4�̏ꍇ������܂��B�ȉ��ł́Ak�Cl��0�ȏ�������Ƃ��܂��B
(i) 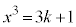 ����
����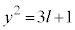 �̂Ƃ��A
�̂Ƃ��A 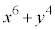 ��9�̔{���ɂȂ邱�Ƃ͂���܂���B
��9�̔{���ɂȂ邱�Ƃ͂���܂���B(ii) 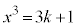 ����
����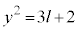 �̂Ƃ��A
�̂Ƃ��A 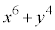 ��9�̔{���ɂȂ邱�Ƃ͂���܂���B
��9�̔{���ɂȂ邱�Ƃ͂���܂���B(iii) 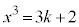 ����
����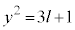 �̂Ƃ��A
�̂Ƃ��A 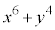 ��9�̔{���ɂȂ邱�Ƃ͂���܂���B
��9�̔{���ɂȂ邱�Ƃ͂���܂���B(iv) 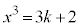 ����
����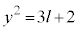 �̂Ƃ��A
�̂Ƃ��A 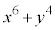 ��9�̔{���ɂȂ邱�Ƃ͂���܂���B
��9�̔{���ɂȂ邱�Ƃ͂���܂���B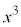 �C
�C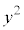 �̂����ꂩ�����3�̔{���ő�����3�̔{���łȂ��Ƃ��́Ak��0�ȏ�̐����Ƃ��āA
�̂����ꂩ�����3�̔{���ő�����3�̔{���łȂ��Ƃ��́Ak��0�ȏ�̐����Ƃ��āA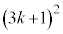 ��
��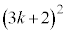 ��3�̔{���ł͂Ȃ��̂ŁA
��3�̔{���ł͂Ȃ��̂ŁA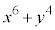 ��9�̔{���ɂȂ邱�Ƃ͂���܂���B
��9�̔{���ɂȂ邱�Ƃ͂���܂���B
����āA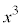 ��
��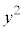 ���Ƃ���3�̔{���ł��B�����Ax�Cy�͂Ƃ���3�̔{���ŁAm�Cn�𐳐����Ƃ��āA
���Ƃ���3�̔{���ł��B�����Ax�Cy�͂Ƃ���3�̔{���ŁAm�Cn�𐳐����Ƃ��āA
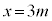 �C
�C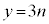 �@����@
�@����@
�ƂȂ鐳����z�́A
�����A���ꂪ�������ł��邽�߂ɂ́A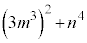 ���������ł���K�v������܂��Bm�Cn�ɏ����������琳�����l�������A
���������ł���K�v������܂��Bm�Cn�ɏ����������琳�����l�������A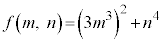 ���������ɂȂ邩�ǂ������ׂ܂��B
���������ɂȂ邩�ǂ������ׂ܂��B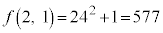 �͕������łȂ��A
�͕������łȂ��A
����͕������ł͂���܂���B
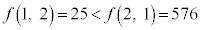 �ł���Am�Cn��傫�������
�ł���Am�Cn��傫�������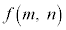 ���傫���Ȃ�̂ŁA����
���傫���Ȃ�̂ŁA����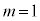 �C
�C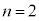 �̏ꍇ��N�̍ŏ��l��^���܂��B
�̏ꍇ��N�̍ŏ��l��^���܂��B
���̂Ƃ��@���A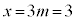 �C
�C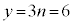
N�̍ŏ��l��2025 ......[��]
���Ȃ݂ɁA2�Ԗڂɏ������̂́A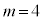 �C
�C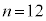 �C
�C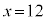 �C
�C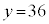 �̂Ƃ���
�̂Ƃ���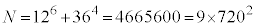 �C
�C
3�Ԗڂɏ������̂́A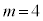 �C
�C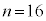 �C
�C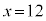 �C
�C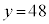 �̂Ƃ���
�̂Ƃ���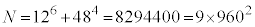 �ł��B
�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B