京都大学理系2025年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 次の各問に答えよ。
問1 iは虚数単位とする。複素数zが、絶対値2である複素数全体を動くとき、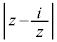 の最大値と最小値を求めよ。
の最大値と最小値を求めよ。 問2 次の定積分の値を求めよ。
(1) 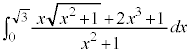 (2)
(2) 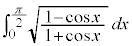
[解答へ]
[2] 正の整数x,y,zを用いて
と表される正の整数Nの最小値を求めよ。
[解答へ]
[3] eは自然対数の底とする。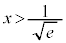 において定義された次の関数
において定義された次の関数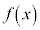 ,
,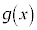 を考える。
を考える。
実数t は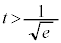 を満たすとする。曲線
を満たすとする。曲線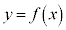 上の点
上の点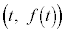 における接線に垂直で、点
における接線に垂直で、点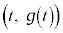 を通る直線
を通る直線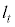 とする。直線
とする。直線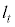 がx軸と交わる点のx座標を
がx軸と交わる点のx座標を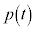 とする。t が
とする。t が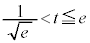 の範囲を動くとき、
の範囲を動くとき、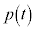 の取りうる値の範囲を求めよ。
の取りうる値の範囲を求めよ。
[解答へ]
[4] 座標空間の4点O,A,B,Cは同一平面上にないとする。s,t,uは0でない実数とする。直線OA上の点L,直線OB上の点M,直線OC上の点Nを
が成り立つようにとる。
(1) s,t,uが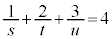 を満たす範囲であらゆる値をとるとき、3点L,M,Nの定める平面LMNは、s,t,uの値に無関係な一定の点Pを通ることを示せ。さらに、そのような点Pはただ一つに定まることを示せ。
を満たす範囲であらゆる値をとるとき、3点L,M,Nの定める平面LMNは、s,t,uの値に無関係な一定の点Pを通ることを示せ。さらに、そのような点Pはただ一つに定まることを示せ。 (2) 四面体OABCの体積をVとする。(1)における点Pについて、四面体PABCの体積をVを用いて表せ。
[解答へ]
[5] θは実数とする。xyz空間の2点A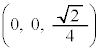 ,P
,P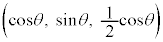 を通る直線APがxy平面と交わるとき、その交点をQとする。θが
を通る直線APがxy平面と交わるとき、その交点をQとする。θが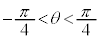 の範囲を動くときの点Qの軌跡を求め、その軌跡をxy平面上に図示せよ。
の範囲を動くときの点Qの軌跡を求め、その軌跡をxy平面上に図示せよ。
[解答へ]
[6] nは2以上の整数とする。1枚の硬貨を続けてn回投げる。このとき、k回目(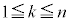 )に表が出たら
)に表が出たら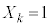 ,裏が出たら
,裏が出たら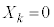 として、
として、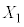 ,
,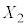 ,・・・,
,・・・,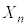 を定める。
を定める。
とするとき、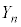 が奇数である確率
が奇数である確率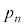 を求めよ。
を求めよ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
京大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2025(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 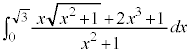 (2)
(2) 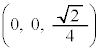 ,P
,P