���嗝�n���w'25�N�O��[6]
n��2�ȏ�̐����Ƃ���B1���̍d�݂𑱂���n����B���̂Ƃ��Ak���(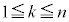 )�ɕ\���o����
)�ɕ\���o����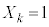 �C�����o����
�C�����o����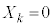 �Ƃ��āA
�Ƃ��āA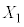 �C
�C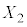 �C����C
�C����C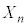 ���߂�B
���߂�B
�Ƃ���Ƃ��A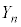 ����ł���m��
����ł���m��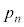 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@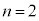 �̏ꍇ�A
�̏ꍇ�A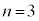 �̏ꍇ�A
�̏ꍇ�A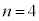 �̏ꍇ����̓I�ɒ��ׂčs���ƁA���̃J���N���������Ă��܂��B
�̏ꍇ����̓I�ɒ��ׂčs���ƁA���̃J���N���������Ă��܂��B
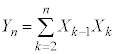 �@����@
�@����@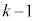 ��ځAk��ڂɁ����Ƒ����Ƃ���
��ځAk��ڂɁ����Ƒ����Ƃ���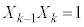 �ƂȂ�܂��B
�ƂȂ�܂��B
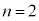 �̂Ƃ��A�@�́A
�̂Ƃ��A�@�́A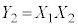 �C�d�݂̏o���͈ȉ���4�ʂ肠��܂��B
�C�d�݂̏o���͈ȉ���4�ʂ肠��܂��B�����@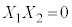
���Z�@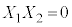
�Z���@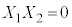
�Z�Z�@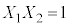
����āA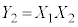 ����ɂȂ��m��
����ɂȂ��m��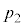 �́A
�́A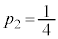 �@����@
�@����@ 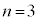 �̂Ƃ��A�@�́A
�̂Ƃ��A�@�́A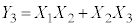 �C�d�݂̏o���͈ȉ���8�ʂ肠��܂��B
�C�d�݂̏o���͈ȉ���8�ʂ肠��܂��B�������@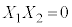 �C
�C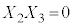 �C
�C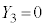
�����Z�@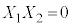 �C
�C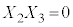 �C
�C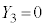
���Z���@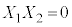 �C
�C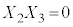 �C
�C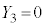
�������@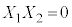 �C
�C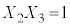 �C
�C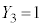
�������@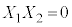 �C
�C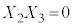 �C
�C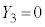
�������@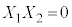 �C
�C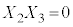 �C
�C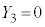
�������@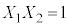 �C
�C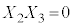 �C
�C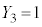
�������@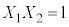 �C
�C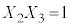 �C
�C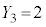
����āA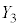 ����ɂȂ�m��
����ɂȂ�m��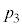 �́A
�́A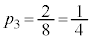 �@����A
�@����A 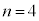 �̂Ƃ��A�@�́A
�̂Ƃ��A�@�́A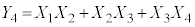 �C�d�݂̏o���͈ȉ���16�ʂ肠��܂��B
�C�d�݂̏o���͈ȉ���16�ʂ肠��܂��B���������@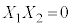 �C
�C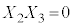 �C
�C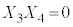 �C
�C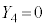
���������@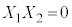 �C
�C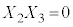 �C
�C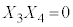 �C
�C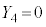
���������@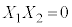 �C
�C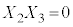 �C
�C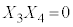 �C
�C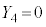
���������@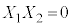 �C
�C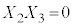 �C
�C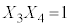 �C
�C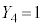
���������@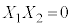 �C
�C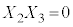 �C
�C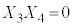 �C
�C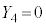
���������@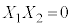 �C
�C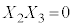 �C
�C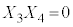 �C
�C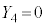
���������@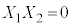 �C
�C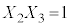 �C
�C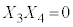 �C
�C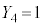
���������@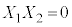 �C
�C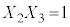 �C
�C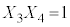 �C
�C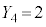
���������@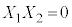 �C
�C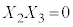 �C
�C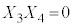 �C
�C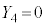
���������@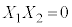 �C
�C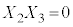 �C
�C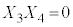 �C
�C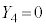
���������@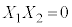 �C
�C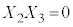 �C
�C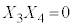 �C
�C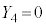
���������@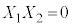 �C
�C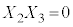 �C
�C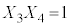 �C
�C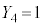
���������@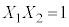 �C
�C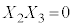 �C
�C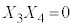 �C
�C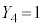
���������@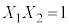 �C
�C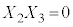 �C
�C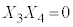 �C
�C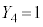
���������@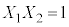 �C
�C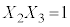 �C
�C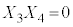 �C
�C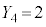
���������@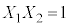 �C
�C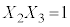 �C
�C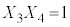 �C
�C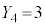
����āA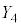 ����ɂȂ�m��
����ɂȂ�m��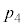 �́A
�́A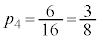 �@����B
�@����B 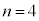 �̂Ƃ�������ƁAn��d�ݓ���������
�̂Ƃ�������ƁAn��d�ݓ���������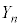 ����ɂȂ�̂́A
����ɂȂ�̂́A
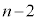 ��d�ݓ���������
��d�ݓ���������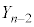 ������(��L�ł́A�ŏ���2��ŏ��Ȃ��Ƃ���������̂Ƃ��ŁA�m��
������(��L�ł́A�ŏ���2��ŏ��Ȃ��Ƃ���������̂Ƃ��ŁA�m��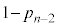 )�ŁA
)�ŁA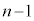 ��ځAn��ڂŁ����Əo��Ƃ�(�m��
��ځAn��ڂŁ����Əo��Ƃ�(�m��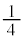 )�A
)�A
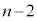 ��d�ݓ���������
��d�ݓ���������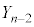 ���(��L�ł́A�ŏ���2�����̂Ƃ��ŁA�m��
���(��L�ł́A�ŏ���2�����̂Ƃ��ŁA�m��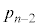 )�ŁA
)�ŁA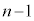 ��ڂ����A�܂��́A
��ڂ����A�܂��́A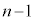 ��ځAn��ڂ������̂Ƃ�(�m��
��ځAn��ڂ������̂Ƃ�(�m��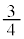 )�A
)�A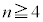 �Ƃ��āA
�Ƃ��āA
k��2�ȏ�̐����Ƃ��āA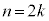 �̂Ƃ��A
�̂Ƃ��A �D�|�E���A
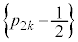 (
(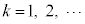 )�́A����
)�́A����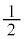 �C����
�C����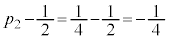 �����䐔���ł��B
�����䐔���ł��B
�@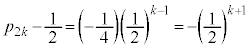
�� 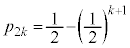 �@����F
�@����F
���̌��ʂ́A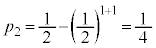 �C
�C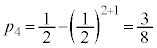 ���@�C�B�����Ă��āA
���@�C�B�����Ă��āA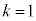 �̂Ƃ��ɂ����藧���܂��B
�̂Ƃ��ɂ����藧���܂��B
���l�ɁAk��2�ȏ�̐����Ƃ��āA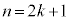 �̂Ƃ��A�C���A
�̂Ƃ��A�C���A
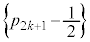 (
(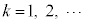 )�́A����
)�́A����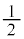 �C����
�C����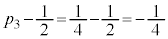 �̓��䐔��ł��B
�̓��䐔��ł��B
�@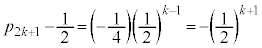
�� 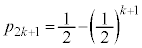 �@����G
�@����G
���̌��ʂ́A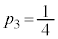 ���A�����Ă��āA
���A�����Ă��āA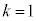 �̂Ƃ��ɂ����藧���܂��B
�̂Ƃ��ɂ����藧���܂��B
k�����R���Ƃ��āA
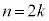 �̂Ƃ��A
�̂Ƃ��A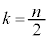 �C�F���A
�C�F���A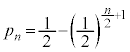
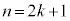 �̂Ƃ��A
�̂Ƃ��A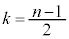 �C�G���A
�C�G���A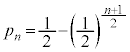 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 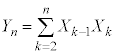
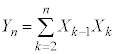 �@����@
�@����@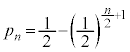
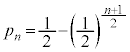 ......[��]
......[��]