���嗝�n���w'25�N�O��[4]
���W��Ԃ�4�_O�CA�CB�CC�͓��ꕽ�ʏ�ɂȂ��Ƃ���Bs�Ct�Cu��0�łȂ������Ƃ���B����OA��̓_L�C����OB��̓_M�C����OC��̓_N��
�����藧�悤�ɂƂ�B
(1) s�Ct�Cu��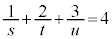 �����͈͂ł�����l���Ƃ�Ƃ��A3�_L�CM�CN�̒�߂镽��LMN�́As�Ct�Cu�̒l�ɖ��W�Ȉ��̓_P��ʂ邱�Ƃ������B����ɁA���̂悤�ȓ_P�͂�����ɒ�܂邱�Ƃ������B
�����͈͂ł�����l���Ƃ�Ƃ��A3�_L�CM�CN�̒�߂镽��LMN�́As�Ct�Cu�̒l�ɖ��W�Ȉ��̓_P��ʂ邱�Ƃ������B����ɁA���̂悤�ȓ_P�͂�����ɒ�܂邱�Ƃ������B (2) �l�ʑ�OABC�̑̐ς�V�Ƃ���B(1)�ɂ�����_P�ɂ��āA�l�ʑ�PABC�̑̐ς�V��p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�R���R���ƃJ���L��������ύX���镶�ȏȂɒ����𑗂�t�������Ȃ�A�ƌ��������Ȗ��ł��B�Ȃ��A��ԃx�N�g�����Q�Ƃ��Ă��������B
��蕶��
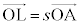 �C
�C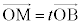 �C
�C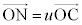 �@(s�Ct�Cu��0�łȂ�����)
�@(s�Ct�Cu��0�łȂ�����)
(1) ����LMN��̓_Q�́Ap�Cq�Cr��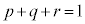 ���������Ƃ��āA
���������Ƃ��āA 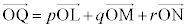 �@����A
�@����A�ƂȂ�܂����A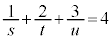 ���
���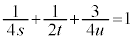 �ł����āA
�ł����āA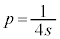 �C
�C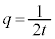 �C
�C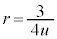 �Ƃ݂�ƁA�B���A
�Ƃ݂�ƁA�B���A 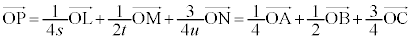 �@����C
�@����C�Ƃ��ĕ\����_P�́A����LMN��̒�_�ł����āA����LMN�́As�Ct�Cu�̒l�ɖ��W�Ȉ��̓_P��ʂ邱�Ƃ��Ӗ����܂��B�܂��A4�_O�CA�CB�CC�͓��ꕽ�ʏ�ɂȂ��̂ŁA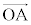 �C
�C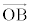 �C
�C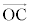 ��1���Ɨ��ł����āA�C�Œ�܂�_P�́A������ɒ�܂�܂��B
��1���Ɨ��ł����āA�C�Œ�܂�_P�́A������ɒ�܂�܂��B
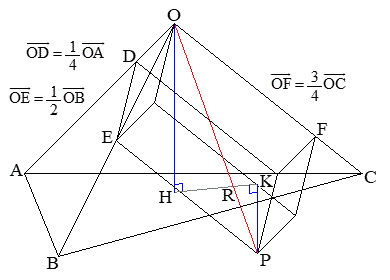 (2) O���灢ABC�ɉ����������̑���H�C��ABC�̖ʐς�S�Ƃ���ƁA�l�ʑ�OABC�̑̐�V��(�l�ʑ̂̑̐����Q��)�A
(2) O���灢ABC�ɉ����������̑���H�C��ABC�̖ʐς�S�Ƃ���ƁA�l�ʑ�OABC�̑̐�V��(�l�ʑ̂̑̐����Q��)�A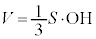 �@����D
�@����D��ABC���܂ޕ��ʂƒ���OP�Ƃ̌�_��R�Ƃ���ƁAk�������Ƃ���(�E�}�Q�ƁA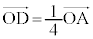 �C
�C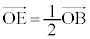 �C
�C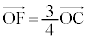 )�A
)�A R�́�ABC���܂ޕ��ʏ�̓_�Ȃ̂ŁA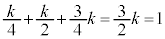 �@��
�@�� 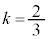
P���灢ABC�ɉ����������̑���K�Ƃ��āA��ORH �� ��PRK���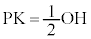 �@����E
�@����E
�l�ʑ�PABC�̑̐�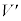 �́A�D�C�E���A
�́A�D�C�E���A 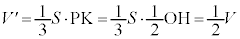 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B