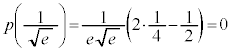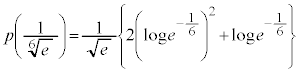���嗝�n���w'25�N�O��[3]
e�͎��R�ΐ��̒�Ƃ���B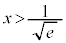 �ɂ����Ē�`���ꂽ���̊�
�ɂ����Ē�`���ꂽ���̊�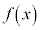 �C
�C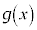 ���l����B
���l����B
����t ��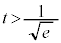 �����Ƃ���B�Ȑ�
�����Ƃ���B�Ȑ�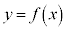 ��̓_
��̓_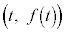 �ɂ�����ڐ��ɐ����ŁA�_
�ɂ�����ڐ��ɐ����ŁA�_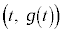 ��ʂ钼��
��ʂ钼��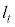 �Ƃ���B����
�Ƃ���B����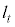 ��x���ƌ����_��x���W��
��x���ƌ����_��x���W��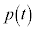 �Ƃ���Bt ��
�Ƃ���Bt ��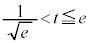 �͈̔͂��Ƃ��A
�͈̔͂��Ƃ��A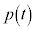 �̎�肤��l�͈̔͂����߂�B
�̎�肤��l�͈̔͂����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�����̌v�Z���ł��B
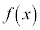 ������������(�ς̔����@���Q��)�A
������������(�ς̔����@���Q��)�A
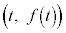 �ɂ������ڐ��̌X����
�ɂ������ڐ��̌X����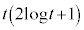 �C���̌X����
�C���̌X����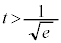 �ɂ�����0�ɂȂ�Ȃ����Ƃɒ��ӂ���ƁA����
�ɂ�����0�ɂȂ�Ȃ����Ƃɒ��ӂ���ƁA����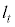 �͐ڐ��Ɛ����Ȃ̂ŁA
�͐ڐ��Ɛ����Ȃ̂ŁA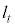 �̌X���́A
�̌X���́A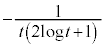
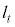 �̕��������A
�̕��������A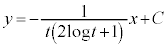 �Ƃ����ƁA
�Ƃ����ƁA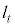 ��
��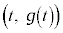 ��ʂ�̂ŁA
��ʂ�̂ŁA
����āA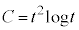
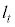 �F
�F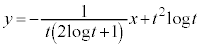 �@����@
�@����@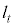 ��x���ƌ����_��x���W�́A�@��
��x���ƌ����_��x���W�́A�@��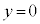 �Ƃ���ƁA
�Ƃ���ƁA
�� 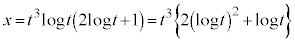
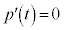 �Ƃ���ƁA
�Ƃ���ƁA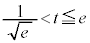 �C�����A
�C�����A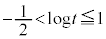 �ɂ����Ă�
�ɂ����Ă�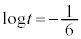 �C
�C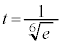
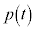 �������\�͈ȉ��̂悤�ɂȂ�܂��B
�������\�͈ȉ��̂悤�ɂȂ�܂��B
�����\���A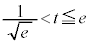 �ɂ�����
�ɂ�����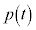 �̎�肤��l�͈̔͂́A
�̎�肤��l�͈̔͂́A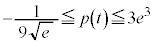 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B