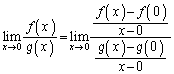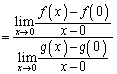���s�^���̒藝�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
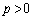 �Ƃ��āA���
�Ƃ��āA���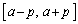 �ɂ������A���ł��A
�ɂ������A���ł��A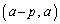 �C
�C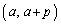 �ɂ����������\�Ȋ�
�ɂ����������\�Ȋ�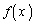 �C
�C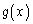 �ɂ��āA
�ɂ��āA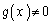 (
(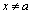 �ɂ�����)�C
�ɂ�����)�C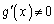 �C
�C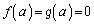 �ł���Ƃ��A
�ł���Ƃ��A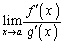 �����݂���A
�����݂���A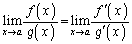
[�ؖ�]�@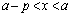 �Ȃ�C�ӂ�x�ɂ��āA
�Ȃ�C�ӂ�x�ɂ��āA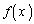 �C
�C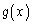 �́A
�́A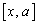 �ɂ����ĘA���ł��A
�ɂ����ĘA���ł��A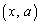 �ɂ����Ĕ����\�ŁA
�ɂ����Ĕ����\�ŁA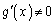 ���A�R�[�V�[�����ϒl�̒藝�̗v�������܂��B����āA
���A�R�[�V�[�����ϒl�̒藝�̗v�������܂��B����āA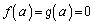 �ƃR�[�V�[�̕��ϒl�̒藝���A
�ƃR�[�V�[�̕��ϒl�̒藝���A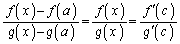 �C
�C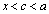 ����c�����݂��܂��B
����c�����݂��܂��B
�����ŁA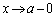 �Ƃ���ƁA
�Ƃ���ƁA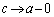
�� 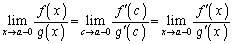 �@����@
�@����@
�܂��A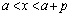 �Ȃ�C�ӂ�x�ɂ��āA
�Ȃ�C�ӂ�x�ɂ��āA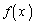 �C
�C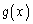 �́A
�́A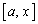 �ɂ����ĘA���ł��A
�ɂ����ĘA���ł��A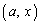 �ɂ����Ĕ����\�ŁA
�ɂ����Ĕ����\�ŁA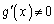 ���A�R�[�V�[�̕��ϒl�̒藝�̗v�������܂��B����āA
���A�R�[�V�[�̕��ϒl�̒藝�̗v�������܂��B����āA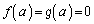 �ƃR�[�V�[�̕��ϒl�̒藝���A
�ƃR�[�V�[�̕��ϒl�̒藝���A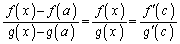 �C
�C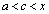 ����c�����݂��܂��B
����c�����݂��܂��B
�����ŁA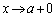 �Ƃ���ƁA
�Ƃ���ƁA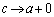
�� 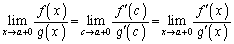 �@����A
�@����A
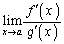 �����݂���A
�����݂���A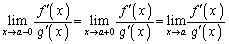
����āA�@�C�A���A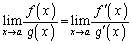 �@(�ؖ��I)
�@(�ؖ��I)
��L�Ɠ��l�ɂ��āA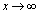 �C
�C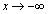 �̏ꍇ�ɂ��Ă��A���l�̂��Ƃ������܂��B
�̏ꍇ�ɂ��Ă��A���l�̂��Ƃ������܂��B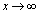 �ɂ��Ă͈ȉ��̂悤�ɂȂ�܂�(
�ɂ��Ă͈ȉ��̂悤�ɂȂ�܂�(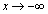 �����l�ł�)�B
�����l�ł�)�B
���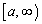 �ɂ����ĘA�����A
�ɂ����ĘA�����A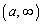 �ɂ����Ĕ����\�Ȋ�
�ɂ����Ĕ����\�Ȋ�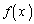 �C
�C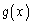 �ɂ��āA
�ɂ��āA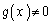 �C
�C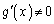 �C
�C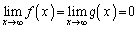 �ł���Ƃ��A
�ł���Ƃ��A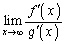 �����݂���A
�����݂���A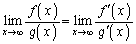
[�ؖ�]�@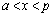 �Ȃ�C�ӂ�x�Cp�ɂ��āA
�Ȃ�C�ӂ�x�Cp�ɂ��āA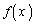 �C
�C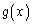 �́A
�́A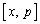 �ɂ����ĘA���ł��A
�ɂ����ĘA���ł��A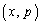 �ɂ����Ĕ����\�ŁA
�ɂ����Ĕ����\�ŁA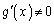 ���A�R�[�V�[�̕��ϒl�̒藝�̗v�������܂��B����āA�R�[�V�[�̕��ϒl�̒藝���A
���A�R�[�V�[�̕��ϒl�̒藝�̗v�������܂��B����āA�R�[�V�[�̕��ϒl�̒藝���A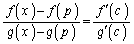 �C
�C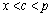 ����c�����݂��܂��B
����c�����݂��܂��B
�����ŁA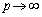 �Ƃ��Ă���A
�Ƃ��Ă���A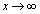 �Ƃ���A
�Ƃ���A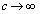 �ł����āA
�ł����āA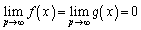 ���A
���A
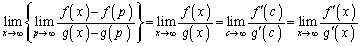 �@(�ؖ��I)
�@(�ؖ��I)
�܂��A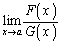 �C
�C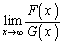 �ɂ����āA
�ɂ����āA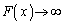 �C
�C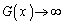 �ƂȂ��Ă��܂��ꍇ�ɂ́A
�ƂȂ��Ă��܂��ꍇ�ɂ́A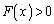 �C
�C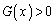 �����藧�͈͂ɂ����āA
�����藧�͈͂ɂ����āA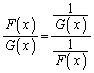 �Ƃ��A
�Ƃ��A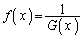 �C
�C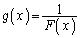 �Ƃ���A
�Ƃ���A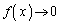 �C
�C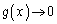 �ƂȂ��āA���s�^���̒藝���g�����Ƃ��ł��܂��B
�ƂȂ��āA���s�^���̒藝���g�����Ƃ��ł��܂��B
���s�^���̒藝���s��`�̋Ɍ������߂�ꍇ�Ɏg���܂��B
��D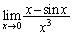 �́A
�́A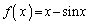 �C
�C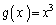 �Ƃ݂�ƁA���s�^���̒藝�̗v�������̂ŁA
�Ƃ݂�ƁA���s�^���̒藝�̗v�������̂ŁA
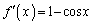 �C
�C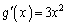 �C���s�^���̒藝���A
�C���s�^���̒藝���A
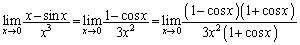
�@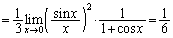
�Ƃ��ċ��߂邱�Ƃ��ł��܂��B
��w�����ɂ����āA���s�^���̒藝�́A�̂ݗv������Ă���ꍇ�ɂ͕֗��ł����A���Z�̋��ȏ��ɍڂ��Ă��Ȃ��̂ŁA�_�q���̓��ĂɎg���Ă��悢�̂��Ƃ����S�z������܂��B
���̂Ƃ��ɂ́A�ȉ��̂悤�ɂ��āA�u���s�^���̒藝���v�Ƃ����������������肪����܂��B
��L��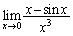 �Ƃ����悤���s��`�̋Ɍ��̗�̏ꍇ�A
�Ƃ����悤���s��`�̋Ɍ��̗�̏ꍇ�A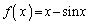 �C
�C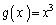 �Ƃ��āA
�Ƃ��āA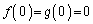 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA
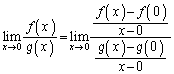
�@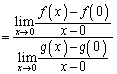
�@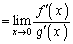
�Ƃ��āA
�� 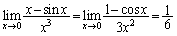
�Ƃ����OK�ł��B
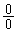 �C
�C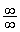 �^���s��`�ŋɌ������܂����߂��Ȃ��Ƃ��́A���̎肪�g���܂��B
�^���s��`�ŋɌ������܂����߂��Ȃ��Ƃ��́A���̎肪�g���܂��B
��L�̗�ł́A���s�^���̒藝���g��Ȃ��̂ł���A�s����
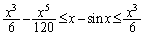 �@(
�@(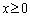 )
)
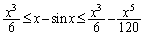 �@(
�@(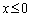 )
)
���ؖ������͂��݂����ɂ��邵������܂���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 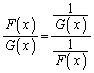 �Ƃ��A
�Ƃ��A