�ɍ��W�̃O���t
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���낢��ȋȐ��Ƃ������ڂ̒��ŁA�ɕ������ŕ\���ꂽ�Ȑ����R���s���[�^�[�ɏ����������̂������܂����B
�����ł́A��w�������ŁA�ɕ������ŕ\���ꂽ�Ȑ��̊T�`��}��������@���A���}�\���F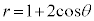 ���ɂƂ��āA�����Ă����܂��B
���ɂƂ��āA�����Ă����܂��B
 �܂��Aθ ����x���Ar����y���̂悤��(�������W�n�̂悤��)�Ƃ��āA
�܂��Aθ ����x���Ar����y���̂悤��(�������W�n�̂悤��)�Ƃ��āA
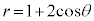
�̃O���t���E�}�̂悤�ɏ����܂��B
����́A�O�p���̃O���t(�����Ȑ�)�Ȃ̂ł��������܂��B �ɂ����ẮA
�ɂ����ẮA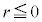 �Ȃ̂ŁA�O���t��θ ���̉��ɗ��܂��B
�Ȃ̂ŁA�O���t��θ ���̉��ɗ��܂��B
���t�Ȑ��F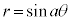 �̂悤�ȏꍇ�Aa�̒l�ɂ���ẮA
�̂悤�ȏꍇ�Aa�̒l�ɂ���ẮA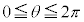 �͈̔͂����ł͕s������\��������A
�͈̔͂����ł͕s������\��������A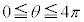 �Ƃ�
�Ƃ�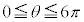 �Ȃǂ͈̔͂ŏ����K�v���o�Ă���ꍇ������܂��B
�Ȃǂ͈̔͂ŏ����K�v���o�Ă���ꍇ������܂��B
���邢�́A���\�̂悤�ȕ\�����܂��B
| θ | 0 | 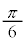 | 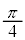 | 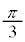 | 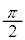 | 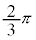 | 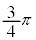 | 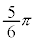 | π | 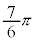 | 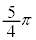 | 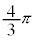 | 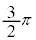 | 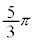 | 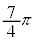 | 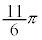 | 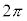 |
| r | 3 | 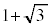 | 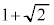 | 2 | 1 | 0 | 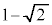 | 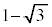 | 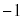 | 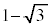 | 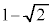 | 0 | 1 | 2 | 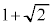 | 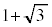 | 3 |
| �@ | �A | �B | �C | �D | �E | �F | �G | �H |
|
|
|
|
|
|
|
|
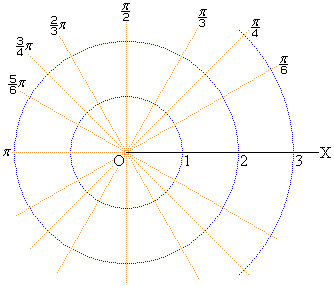 �ɍ��W�n�ŃO���t�������ꍇ�ɂ́A�E�}�̂悤�ɁA��O�𒆐S�Ƃ��铯�S�~��
�ɍ��W�n�ŃO���t�������ꍇ�ɂ́A�E�}�̂悤�ɁA��O�𒆐S�Ƃ��铯�S�~��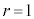 �C
�C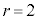 �C
�C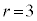 �ȂǁA�K�v�ɉ����ď����Ă����܂��B
�ȂǁA�K�v�ɉ����ď����Ă����܂��B
�܂��A�ɂ�ʂ钼��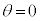 �C
�C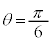 �C
�C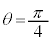 �C
�C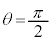 �C
�C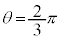 �C
�C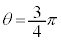 �C
�C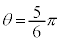 �ȂǁA�K�v�ɉ����ď����Ă����܂��B
�ȂǁA�K�v�ɉ����ď����Ă����܂��B
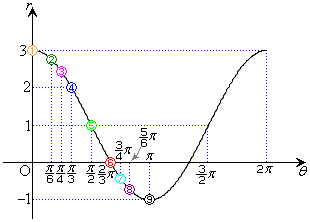
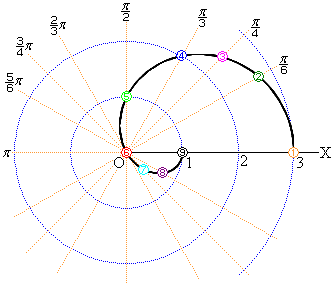 ���}�\���F
���}�\���F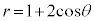 �ł́A
�ł́A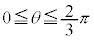 �ɂ����Ă�
�ɂ����Ă�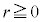 �ł��B�O���t�A���邢�́A�\���Q�l�ɁAθ �̒l�Œ�܂�ɂ�ʂ钼����̋ɂ���̋�����r�̂Ƃ���ɓ_���v���b�g���čs���܂��B�E�}�ł́A�@�`�E�Ŏ����܂����B
�ł��B�O���t�A���邢�́A�\���Q�l�ɁAθ �̒l�Œ�܂�ɂ�ʂ钼����̋ɂ���̋�����r�̂Ƃ���ɓ_���v���b�g���čs���܂��B�E�}�ł́A�@�`�E�Ŏ����܂����B
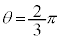 �̂Ƃ��ɁA�v���b�g����_�͋�O�ɗ��܂�(�E)�B
�̂Ƃ��ɁA�v���b�g����_�͋�O�ɗ��܂�(�E)�B
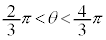 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A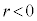 �ƂȂ�܂��B���̂Ƃ��ɂ́A
�ƂȂ�܂��B���̂Ƃ��ɂ́A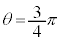 �ł���A
�ł���A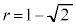 �ł����A�ɂ��獶��Ƀ}�C�i�X�i�Ƃ���ƍl���āA�E���̕���(
�ł����A�ɂ��獶��Ƀ}�C�i�X�i�Ƃ���ƍl���āA�E���̕���(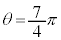 �̕���)��
�̕���)��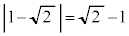 �i�Ƃ���ɓ_���v���b�g���܂�(�F)�B
�i�Ƃ���ɓ_���v���b�g���܂�(�F)�B
���̂悤�ɁA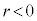 �̏ꍇ�ɂ́A��O����t�����ɋ���
�̏ꍇ�ɂ́A��O����t�����ɋ���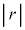 �̂Ƃ���ɓ_���v���b�g���܂��B�E�}�ł́A
�̂Ƃ���ɓ_���v���b�g���܂��B�E�}�ł́A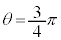 �C
�C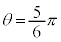 �C
�C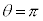 ��3�_�A�F�C�G�C�H���v���b�g���܂����B
��3�_�A�F�C�G�C�H���v���b�g���܂����B
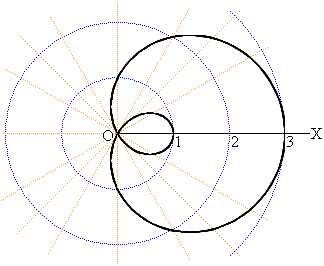
 �͈̔͂̃O���t�́A�ȏ�Ńv���b�g�����_�����炩�ɂȂ��ōs���O���t�������܂��B�Ȑ��ɂ���ẮA��_�ƌ����ĂƂ������_���o�Ă��邱�Ƃ�����܂��B
�͈̔͂̃O���t�́A�ȏ�Ńv���b�g�����_�����炩�ɂȂ��ōs���O���t�������܂��B�Ȑ��ɂ���ẮA��_�ƌ����ĂƂ������_���o�Ă��邱�Ƃ�����܂��B
 ���}�\���F
���}�\���F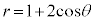 �ł́A
�ł́A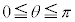 �̕�����
�̕�����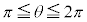 �̕����Ƃ́A�n���Ɋւ��đΏ̂Ȃ̂ŁA
�̕����Ƃ́A�n���Ɋւ��đΏ̂Ȃ̂ŁA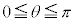 �̕������n���Ɋւ��Đ܂�Ԃ��A�E�}�̂悤�ȃO���t�������܂��B�ɂ̂Ƃ���Ɍ�������Ƃ��낪�ł��܂��B
�̕������n���Ɋւ��Đ܂�Ԃ��A�E�}�̂悤�ȃO���t�������܂��B�ɂ̂Ƃ���Ɍ�������Ƃ��낪�ł��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B