いろいろな曲線
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
(1) トロコイド:半径aの円を、x軸と接したまま滑らずに回転させるとき、中心から距離bの点(円とともに回転する)が描く軌跡。
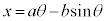 ,
,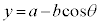
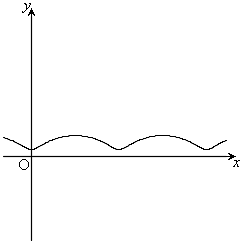
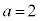 ,
,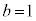 のとき、右図。
のとき、右図。
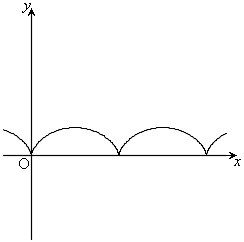
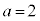 ,
,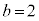 のとき、右図。これは、サイクロイドです。
のとき、右図。これは、サイクロイドです。
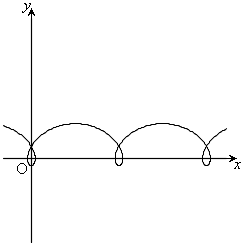
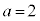 ,
,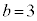 のとき、右図。
のとき、右図。
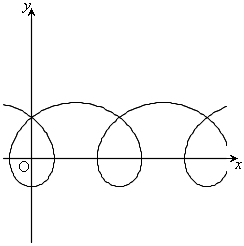
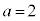 ,
,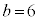 のとき、右図。
のとき、右図。
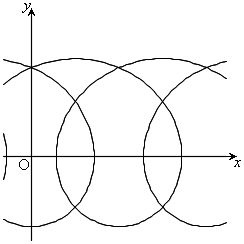
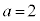 ,
,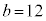 のとき、右図。
のとき、右図。
(2) ハイポトロコイド:半径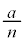 の円Cを、半径aの円周に内接させたまま滑らせずに回転させるとき、円Cの中心から距離bの点(円Cとともに回転する)が描く軌跡。
の円Cを、半径aの円周に内接させたまま滑らせずに回転させるとき、円Cの中心から距離bの点(円Cとともに回転する)が描く軌跡。
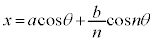 ,
,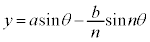
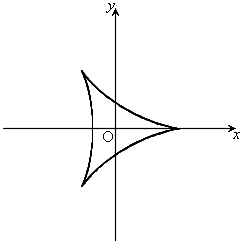
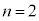 ,
,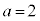 ,
,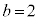 のとき、右図。これは、ハイポサイクロイドです。
のとき、右図。これは、ハイポサイクロイドです。
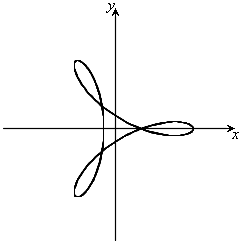
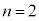 ,
,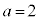 ,
,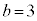 のとき、右図。
のとき、右図。
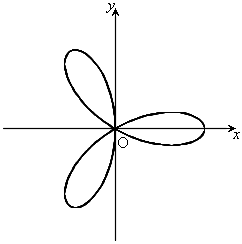
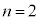 ,
,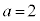 ,
,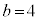 のとき、右図。
のとき、右図。
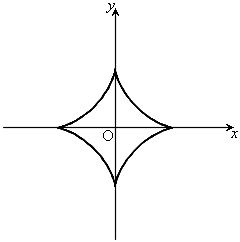
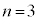 ,
,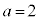 ,
,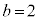 のとき、右図。これは、アステロイドです。
のとき、右図。これは、アステロイドです。
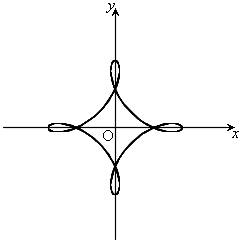
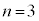 ,
,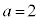 ,
,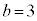 のとき、右図。
のとき、右図。
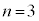 ,
,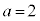 ,
,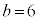 のとき、右図。
のとき、右図。
(3) エピトロコイド:半径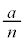 の円Cを、半径aの円に外接させたまま滑らせずに回転させるとき、円Cの中心から距離bの点(円Cとともに回転する)が描く軌跡。
の円Cを、半径aの円に外接させたまま滑らせずに回転させるとき、円Cの中心から距離bの点(円Cとともに回転する)が描く軌跡。
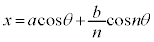 ,
,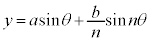
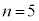 ,
,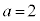 ,
,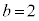 のとき、右図。これは、エピサイクロイドです。
のとき、右図。これは、エピサイクロイドです。
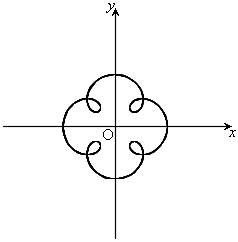
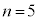 ,
,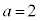 ,
,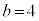 のとき、右図。
のとき、右図。
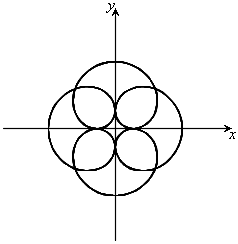
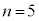 ,
,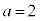 ,
,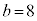 のとき、右図。
のとき、右図。
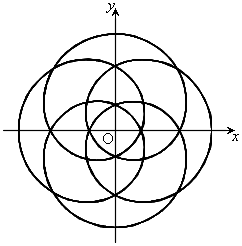
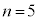 ,
,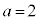 ,
,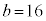 のとき、右図。
のとき、右図。
(4) リサジュー図形
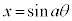 ,
,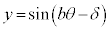
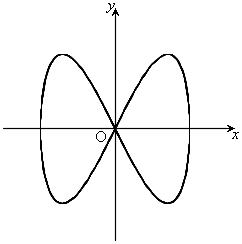
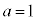 ,
,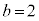 ,
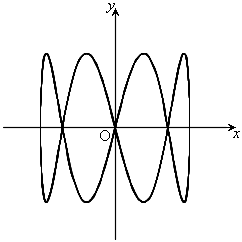
,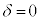 のとき、右図。
のとき、右図。
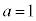 ,
,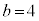 ,
,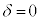 のとき、右図。
のとき、右図。
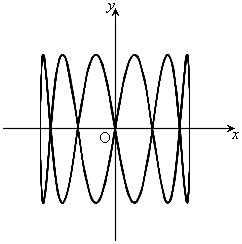
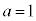 ,
,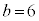 ,
,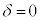 のとき、右図。
のとき、右図。
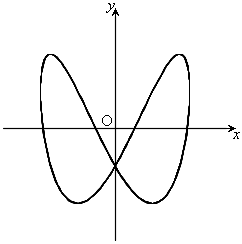
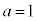 ,
,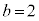 ,
,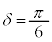 のとき、右図。
のとき、右図。
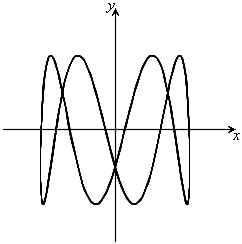
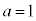 ,
,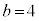 ,
,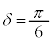 のとき、右図。
のとき、右図。
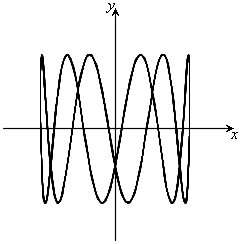
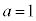 ,
,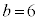 ,
,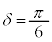 のとき、右図。
のとき、右図。
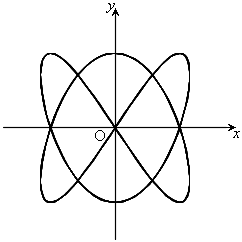
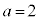 ,
,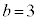 ,
,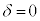 のとき、右図。
のとき、右図。
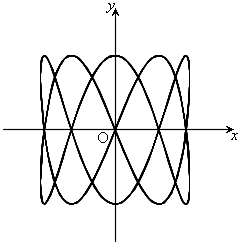
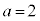 ,
,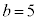 ,
,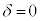 のとき、右図。
のとき、右図。
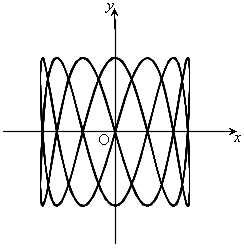
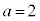 ,
,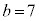 ,
,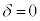 のとき、右図。
のとき、右図。
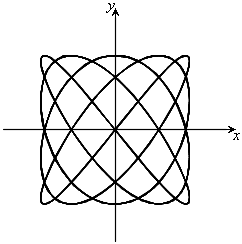
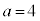 ,
,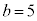 ,
, のとき、右図。
のとき、右図。
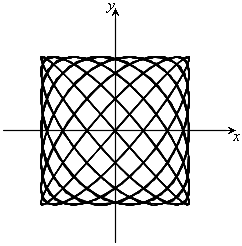
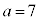 ,
,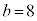 ,
,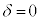 のとき、右図。
のとき、右図。
(5) 螺旋(らせん)
直交座標では、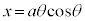 ,
,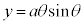 ,極方程式は、
,極方程式は、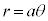 (
(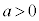 ,
,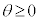 )
)
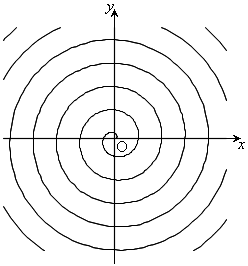
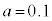 のとき、右図。
のとき、右図。
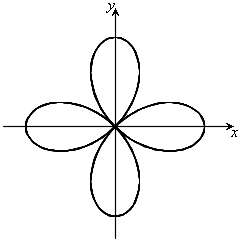
(6) 正葉曲線
直交座標では、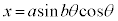 ,
,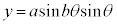 ,極方程式は、
,極方程式は、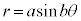 (
(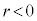 のときは、
のときは、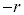 をr,θ を
をr,θ を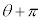 として考える)
として考える)
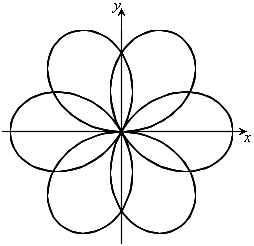
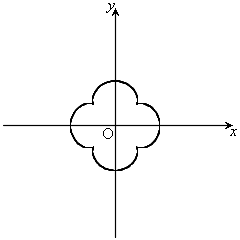
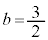 のとき、右図。
のとき、右図。
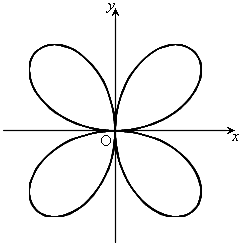
 のとき、右図。
のとき、右図。
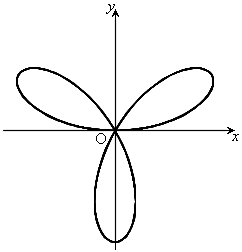
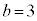 のとき、右図。
のとき、右図。
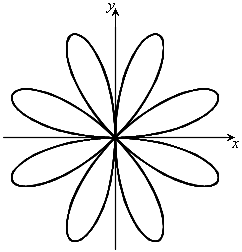
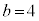 のとき、右図。
のとき、右図。
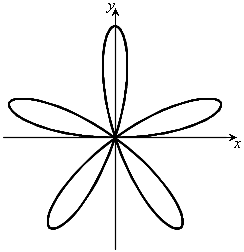
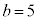 のとき、右図。
のとき、右図。
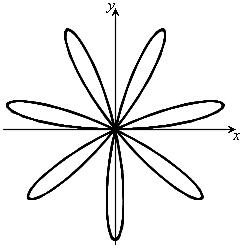
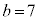 のとき、右図。
のとき、右図。
(7) リマソン
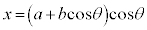 ,
,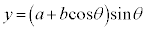 ,極方程式は、
,極方程式は、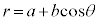 (
(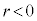 のときは、
のときは、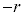 をr,θ を
をr,θ を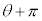 として考える)
として考える)
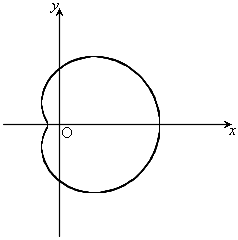
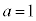 ,
,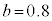 のとき、右図。
のとき、右図。
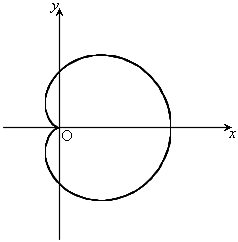
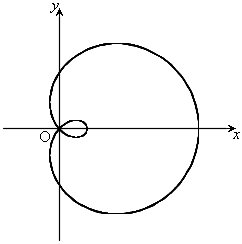
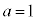 ,
,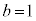 のとき、右図。これは、カージオイドです。
のとき、右図。これは、カージオイドです。
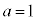 ,
,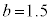 のとき、右図。
のとき、右図。
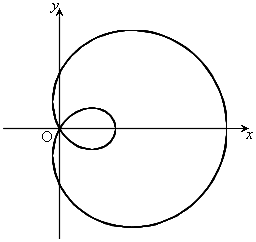
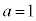 ,
,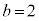 のとき、右図。
のとき、右図。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。