2次曲線に関する問題(その2)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
2次曲線に関する問題(その1)からのつづきです。
2次曲線の問題を2次方程式の問題として扱うと、計算が複雑になりがちです。
ここでは、2次曲線の定義の利用を考えます。
例1．定直線l上を動く1点Hにおいてlと直交する直線と、定点FとHを結ぶ線分の垂直二等分線の交点Pの軌跡を求める。
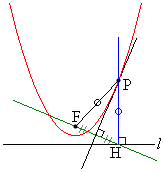[解答] 線分PFと線分PHは、垂直二等分線に関して対称なので、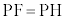
点Pは、定点Fまでの距離と、定直線lまでの距離とが等しい点なので、放物線の定義より、Pの軌跡は、Fを焦点とし、lを準線とする放物線(右図赤線) ......[答]
例2．定直線lに接する円が定点Fを通るとき、この円の中心Cの軌跡を求める。
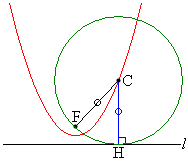[解答] 定直線lと円との接点をHとすると、CFとCHは円の半径で等しい。
よって、点Cは、定点Fまでの距離と、定直線lまでの距離とが等しい点なので、放物線の定義より、Cの軌跡は、Fを焦点とし、lを準線とする放物線(右図赤線) ......[答]
例3．定点Cを中心とする円周上の動点Bと円の内部の定点A (中心Cとは異なる)とを結ぶ線分の垂直二等分線と、線分CBとの交点Pの軌跡を求める。
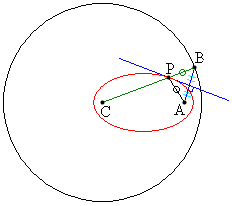[解答] 線分PBと線分PAは、垂直二等分線に関して対称なので、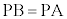
円の半径を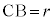
として、
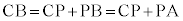より、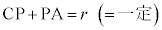
よって、Pは2定点C，Aまでの距離の和がrで一定である点なので、楕円の定義より、Pの軌跡は、2定点C，Aを焦点とし、この円の半径を長軸の長さとする楕円(右図赤線) ......[答]
例4．定点Aを中心とする一定の円周Cに内接し、かつ、円C内のAと異なる定点Bを通る円の中心Pの軌跡を求める。
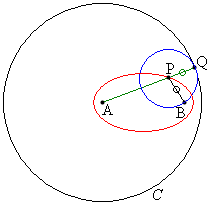[解答] 内接円と円Cとの接点をQとする。A，P，Qは同一直線上の点。PQとPBはともに内接円の半径であって、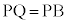
円Cの半径を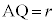
として、
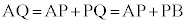より、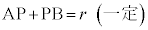
よって、Pは2定点A，Bまでの距離の和がrで一定である点なので、楕円の定義より、Pの軌跡は、2定点A，Bを焦点とし、円Cの半径を長軸の長さとする楕円(右図赤線) ......[答]
例5．定点Cを中心とする円周上の動点Bと円の外部の定点Aとを結ぶ線分の垂直二等分線と、直線CBとの交点Pの軌跡を求める。但し、直線ABが円の接線となる場合を除く。
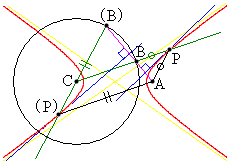[解答] 直線ABが円の接線となる場合には、垂直二等分線が直線CBと平行になり、交点Pが存在しません。
線分PBと線分PAは、垂直二等分線に関して対称なので、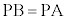
円の半径を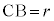
として、
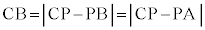より、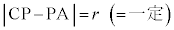
よって、Pは2定点C，Aまでの距離の差がrで一定である点なので、双曲線の定義より、Pの軌跡は、2定点C，Aを焦点とし、この円の半径を双曲線の2つの枝の頂点間の距離とする双曲線 ......[答]
例6．定点Aを中心とする一定の円周Cに外接し、かつ、円C外の定点Bを通る円(が存在すれば)の中心Pの軌跡を求める。
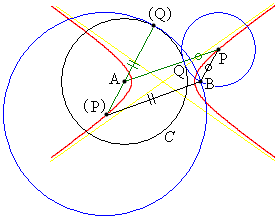[解答] 外接する円と円Cとの接点をQとする。例5と同様に直線BQが円Cの接線になる場合には、外接する円が存在しません。
外接する円が存在すれば、A，P，Qは同一直線上の点。PQとPBはともに外接する円の半径であって、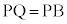
円Cの半径を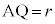
として、
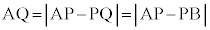より、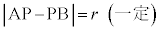
よって、Pは2定点A，Bまでの距離の差がrで一定である点なので、双曲線の定義より、Pの軌跡は、2定点A，Bを焦点とし、円Cの半径を双曲線の2つの枝の頂点間の距離とする双曲線 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。