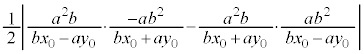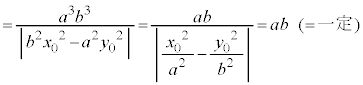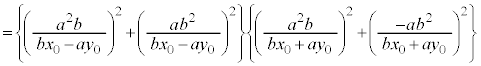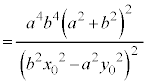2���Ȑ��Ɋւ�����(����1)�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
2���Ȑ��̖���f����2����������p���ĉ����ꍇ�A2���������̔��ʎ��A2���������̉��ƌW���̊W�̋Z�I���l���܂��B
��1�D�ȉ~�F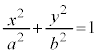 �ƒ����F
�ƒ����F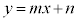 ��2�_P�CQ�Ō�����Ă���Ƃ��Aa�Cb�Cm (
��2�_P�CQ�Ō�����Ă���Ƃ��Aa�Cb�Cm (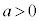 �C
�C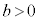 �C
�C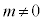 )��萔�Ƃ��āAn�̒l�����Ƃ���PQ�̒��_M���O���A�܂��An�ɑ���PQ�̒��������߂�B
)��萔�Ƃ��āAn�̒l�����Ƃ���PQ�̒��_M���O���A�܂��An�ɑ���PQ�̒��������߂�B
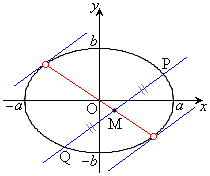 [��]�@�ȉ~�̕������̕�����ƁA
[��]�@�ȉ~�̕������̕�����ƁA
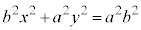
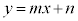 �ƘA�����āA
�ƘA�����āA
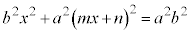
��������ƁA
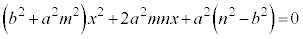 �@����@
�@����@
�ȉ~�ƒ�����2�_�Ō����̂ŁA�@�́A�قȂ�2�������������܂��B
���ʎ��F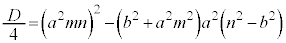
�@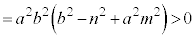 �@(2�����������Q��)
�@(2�����������Q��)
�� 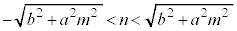
�@��2����α�Cβ �Ƃ���ƁAPQ�̒��_M��x���W��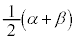 �ł��B
�ł��B
�@�ɂ����āA���ƌW���̊W���A
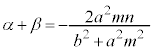
����āAM��x���W�́A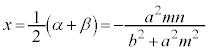 �@����A
�@����A
PQ�̒��_M�́A����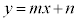 ��̓_�䂦�AM��y���W�́A
��̓_�䂦�AM��y���W�́A
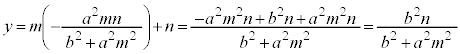 �@����B
�@����B
�A�C�B����n����������ƁA
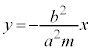
���ꂪ�O�Ղ̕������ł��B
�A�ɂ����āAn�͈̔͂��l������ƁA
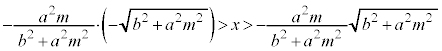
�� 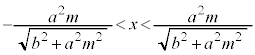
M�̋O�Ղ́A�����F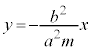 ��
��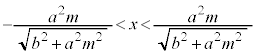 �̕����ŁA�E�}�Ԑ�����(���[���}��������)�B ......[��]
�̕����ŁA�E�}�Ԑ�����(���[���}��������)�B ......[��]
����PQ�̒����́AP�CQ��x���W�̍���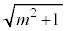 �����������̂ɂȂ�܂��B�܂��AP�CQ��x���W�̍�
�����������̂ɂȂ�܂��B�܂��AP�CQ��x���W�̍�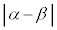 �́A
�́A
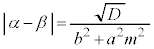 �@(2���������̈�ʘ_���Q�ƁA2���������F
�@(2���������̈�ʘ_���Q�ƁA2���������F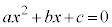 �̔��ʎ���
�̔��ʎ���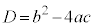 �Ƃ��āA2���̍��́A
�Ƃ��āA2���̍��́A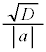 )
)
�@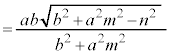
����āAPQ�̒����́A
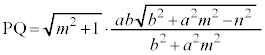 ......[��]
......[��]
��2�D�ȉ~�F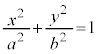 (
(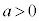 �C
�C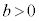 )�O�̓_P����ȉ~�Ɉ�����2�ڐ�����������悤��P�������Ƃ��AP�̋O�Ղ����߂�B
)�O�̓_P����ȉ~�Ɉ�����2�ڐ�����������悤��P�������Ƃ��AP�̋O�Ղ����߂�B
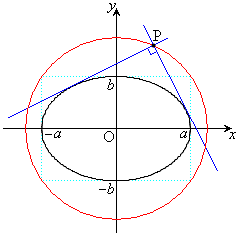 [��]�@
[��]�@ 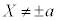 �̂Ƃ��A�_P
�̂Ƃ��A�_P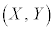 ��ʂ�X��m�̒����́A
��ʂ�X��m�̒����́A
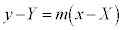
�� 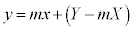 �@����@
�@����@
�ȉ��A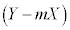 ��1�����̂悤�Ɉ����̂��R�c�ł��B
��1�����̂悤�Ɉ����̂��R�c�ł��B
�ȉ~�̕������̕�����ƁA
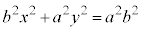
�@��������ƁA
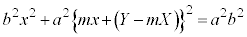
�������āA
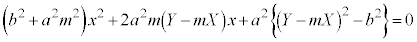
�����@�Ƒȉ~�͐ڂ���̂ŁA����2���������͏d���������A���ʎ��F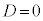 �@(2�����������Q��)
�@(2�����������Q��)
�� 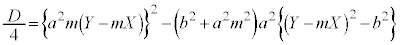
�@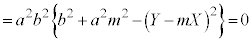
�� 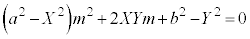
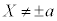 ���A�����m�Ɋւ���2���������ƌ���ƁA2��
���A�����m�Ɋւ���2���������ƌ���ƁA2��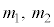 �́AP����ȉ~�Ɉ�����2�ڐ��̌X���ł��B
�́AP����ȉ~�Ɉ�����2�ڐ��̌X���ł��B
2�ڐ�����������̂ŁA�X���̐�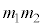 ��
��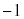 �@(2�����̕��s�Ɛ������Q��)
�@(2�����̕��s�Ɛ������Q��)
���ƌW���̊W���A
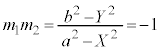
������Đ�������ƁA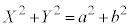 �@����A
�@����A
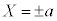 �̂Ƃ��A
�̂Ƃ��A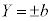 �Ƃ���AP����ȉ~�Ɉ�����2�ڐ��́A
�Ƃ���AP����ȉ~�Ɉ�����2�ڐ��́A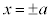 �̂����ꂩ��
�̂����ꂩ��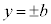 �̂����ꂩ�ł����āA�������܂��B
�̂����ꂩ�ł����āA�������܂��B
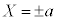 �C
�C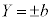 �́A4�ʂ�̕����̂ǂ̑g�ݍ��킹�ɂ��Ă��A�A�����̂ŁA�A�ŁA
�́A4�ʂ�̕����̂ǂ̑g�ݍ��킹�ɂ��Ă��A�A�����̂ŁA�A�ŁA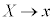 �C
�C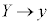 �Ə��������āA
�Ə��������āA
P�̋O�Ղ́A�~�F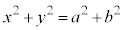 ......[��]
......[��]
���D�~�F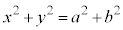 �́A�ȉ~�F
�́A�ȉ~�F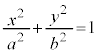 �̏��~�ƌĂ�܂��B
�̏��~�ƌĂ�܂��B
��3�D�������F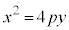 (
(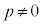 )��ɂȂ��_P����������Ɉ�����2�ڐ�����������悤��P�������Ƃ��AP�̋O�Ղ����߂�B
)��ɂȂ��_P����������Ɉ�����2�ڐ�����������悤��P�������Ƃ��AP�̋O�Ղ����߂�B
[��]�@��2�Ɠ��l�ɁA�_P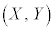 ��ʂ�X��m�̒����́A
��ʂ�X��m�̒����́A
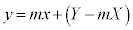 �@����@
�@����@
�������̕������ɑ�����āA
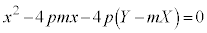
�����@�ƕ��������ڂ���̂ŁA����2���������͏d���������A���ʎ��F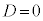
�� 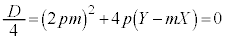
�������āA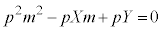
2�ڐ��͒�������̂ŁA����2����������2��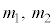 �̐ς́A
�̐ς́A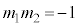
���ƌW���̊W���A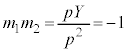
�� 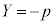
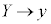 �ƒu�������āAP�̋O�Ղ́A�����F
�ƒu�������āAP�̋O�Ղ́A�����F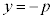 ......[��]
......[��]
�����F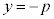 �́A�������F
�́A�������F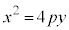 �̏����ł��B
�̏����ł��B
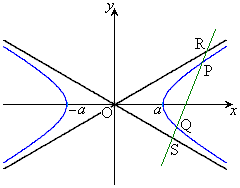
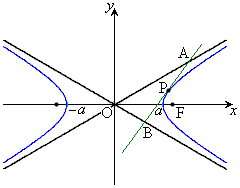
��4�D�o�Ȑ��F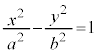 (
(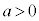 �C
�C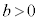 )�Ɋւ��āA�ȉ����ؖ�����B
)�Ɋւ��āA�ȉ����ؖ�����B
(1) �����F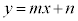 (
(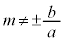 )�ƁA�o�Ȑ��Ƃ̌�_��P�CQ�C�����ƑQ�ߐ��Ƃ̌�_��R�CS�Ƃ��āA
)�ƁA�o�Ȑ��Ƃ̌�_��P�CQ�C�����ƑQ�ߐ��Ƃ̌�_��R�CS�Ƃ��āA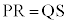
(2) ���_��O�Ƃ���B�o�Ȑ����1�_P�ɂ�����ڐ��ƁA�Q�ߐ��Ƃ̌�_��A�CB�Ƃ���ƁA�_P��AB�̒��_�ł���A�O�p�`OAB�̖ʐς͈��C�܂��A�o�Ȑ��̏œ_��F�Ƃ��āA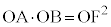
 [�ؖ�](1) �o�Ȑ��̑Q�ߐ��F
[�ؖ�](1) �o�Ȑ��̑Q�ߐ��F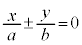 ��
��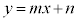 ��A�����A
��A�����A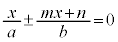
�� 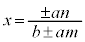 �@(��������)
�@(��������)
����āARS�̒��_��x���W�́A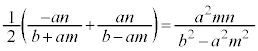
����A�o�Ȑ��̕������̕�����ƁA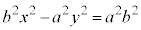
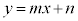 �������āA
�������āA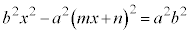
�������āA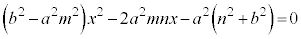
����2����������2��α�Cβ ���AP��Q��x���W�ɂȂ�܂��B
PQ�̒��_��x���W�́A���ƌW���̊W���A
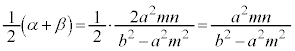
PQ��RS�̒��_����v����̂ŁA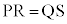 �@(�ؖ��I)
�@(�ؖ��I)
 (2) �ړ_P�̍��W��
(2) �ړ_P�̍��W��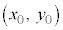 ���Ƃ��āA�ڐ��F
���Ƃ��āA�ڐ��F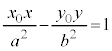
������āA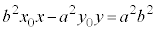
�Q�ߐ��̕������F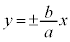 �������āA
�������āA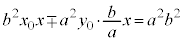
�� 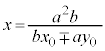 �@(��������)
�@(��������)
����āAAB�̒��_��x���W�́A
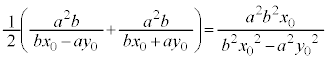
�@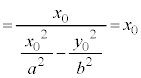 �@(�� P�͑o�Ȑ���̓_������A
�@(�� P�͑o�Ȑ���̓_������A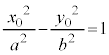 )
)
P�͒���AB��̓_�ł���AAB�̒��_��x���W��P��x���W�Ɉ�v����̂ŁAP��AB�̒��_�ł��B
A�CB��y���W�́Ax���W�̒l��Q�ߐ��̎��ɑ�����邱�Ƃɂ��A
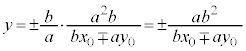 �@(��������)
�@(��������)
�O�p�`OAB�̖ʐς́A
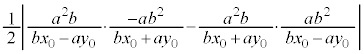
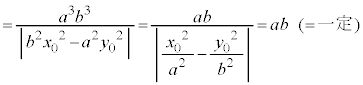
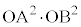
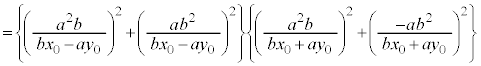
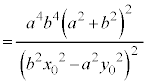
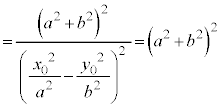
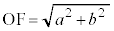 ���A
���A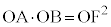 �@(�ؖ��I)
�@(�ؖ��I)
(2���Ȑ��Ɋւ�����(����2)�ւÂ�)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 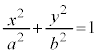 �ƒ����F
�ƒ����F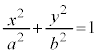 �ƒ����F
�ƒ����F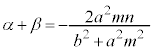
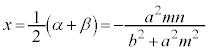 �@����A
�@����A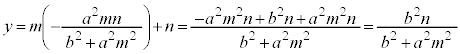 �@����B
�@����B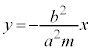
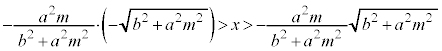
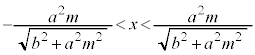
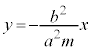 ��
��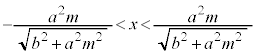 �̕����ŁA�E�}�Ԑ�����(���[���}��������)�B ......[��]
�̕����ŁA�E�}�Ԑ�����(���[���}��������)�B ......[��]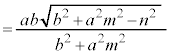
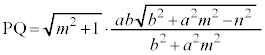 ......[��]
......[��]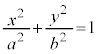 (
(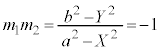
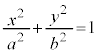 �̏��~�ƌĂ�܂��B
�̏��~�ƌĂ�܂��B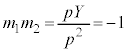
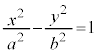 (
(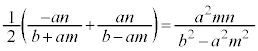
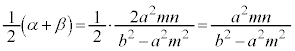
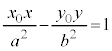
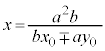 �@(��������)
�@(��������)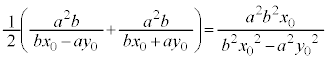
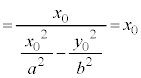 �@(�� P�͑o�Ȑ���̓_������A
�@(�� P�͑o�Ȑ���̓_������A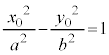 )
)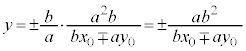 �@(��������)
�@(��������)