無限級数 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
この項目では、数列の極限を参照してください。
数列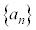 に対して、その各項を加え合わせたものを級数と言う。
に対して、その各項を加え合わせたものを級数と言う。
初項が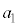 で、有限個(n個)の項からなる数列
で、有限個(n個)の項からなる数列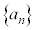 の各項を加え合わせたものを有限級数と言い、有限級数は数列の和:
の各項を加え合わせたものを有限級数と言い、有限級数は数列の和: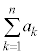 にほかならない。
にほかならない。
初項が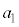 で、無限個の項からなる数列
で、無限個の項からなる数列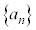 の各項を加え合わせたものを無限級数と言い、
の各項を加え合わせたものを無限級数と言い、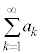 と書く。
と書く。
無限級数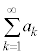 に対して、第n項までの和:
に対して、第n項までの和: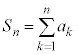 を部分和と言う。
を部分和と言う。
数列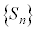 について、
について、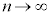 のとき、
のとき、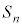 がある値Sに近づくとき、つまり、
がある値Sに近づくとき、つまり、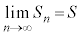 となるとき、“無限級数
となるとき、“無限級数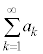 はSに収束する”という言い方をする。また、Sを無限級数
はSに収束する”という言い方をする。また、Sを無限級数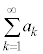 の和と言う。
の和と言う。
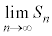 が発散するとき、“無限級数
が発散するとき、“無限級数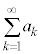 は発散する”という言い方をする。このときには、無限級数は和をもたない。
は発散する”という言い方をする。このときには、無限級数は和をもたない。
例1.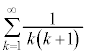 が和をもつなら和を求める。
が和をもつなら和を求める。
[解答] 部分和: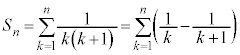
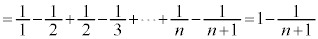
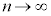 のとき、
のとき、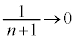 より、
より、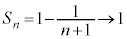
よって、無限級数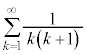 は和をもち、
は和をもち、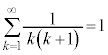 ......[答]
......[答]
例2.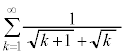 が和をもつなら和を求める。
が和をもつなら和を求める。
[解答] 部分和: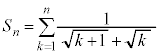
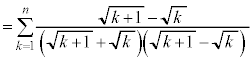
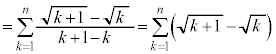
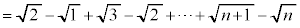
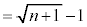
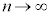 のとき、
のとき、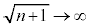 より、
より、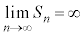
よって、無限級数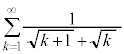 は、和をもたない。
は、和をもたない。
“無限級数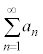 が収束する ⇒
が収束する ⇒ 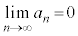 ” は真ですが、
” は真ですが、
“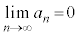 ⇒ 無限級数
⇒ 無限級数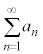 が収束する” は偽です。(条件・命題を参照)
が収束する” は偽です。(条件・命題を参照)
なぜなら、無限級数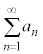 がαに収束するとき、部分和;
がαに収束するとき、部分和;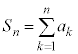 について、
について、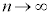 のとき、
のとき、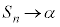 であり、また、
であり、また、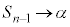
従って、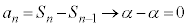
∴ 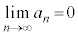
“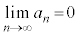 ⇒ 無限級数
⇒ 無限級数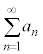 が収束する” の反例は、例2で取り上げた、
が収束する” の反例は、例2で取り上げた、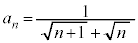 です。
です。
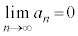 ですが、例2で見たとおり、無限級数
ですが、例2で見たとおり、無限級数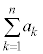 は収束しません。
は収束しません。
k,hを実数として、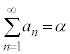 ,
,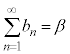 のとき、
のとき、
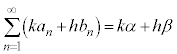
[証明] それぞれの無限級数の部分和を、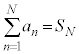 ,
,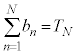 とします。
とします。
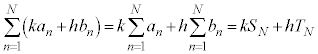 (Σの公式を参照)
(Σの公式を参照)
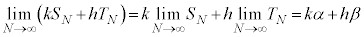 (数列の極限を参照)
(数列の極限を参照)
∴ 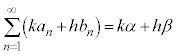 (証明終)
(証明終)
例3.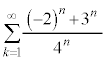 が和をもつなら和を求める。
が和をもつなら和を求める。
[解答] 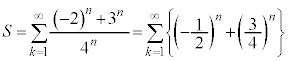
ここで、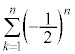 ,
,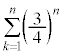 はともに収束するので、
はともに収束するので、
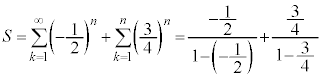 (無限等比級数を参照)
(無限等比級数を参照)
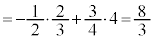 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 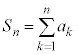 を部分和と言う。
を部分和と言う。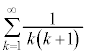 が和をもつなら和を求める。
が和をもつなら和を求める。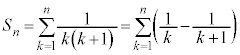
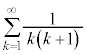 は和をもち、
は和をもち、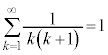 ......[答]
......[答]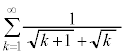 が和をもつなら和を求める。
が和をもつなら和を求める。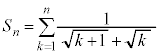
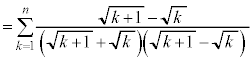
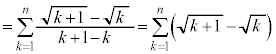
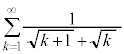 は、和をもたない。
は、和をもたない。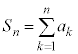 について、
について、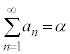 ,
,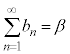 のとき、
のとき、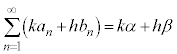
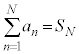 ,
,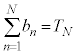 とします。
とします。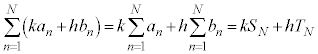 (Σの公式を参照)
(Σの公式を参照)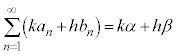 (証明終)
(証明終)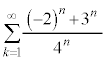 が和をもつなら和を求める。
が和をもつなら和を求める。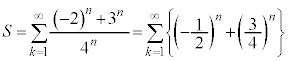
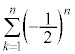 ,
,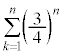 はともに収束するので、
はともに収束するので、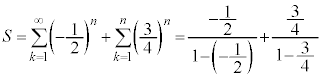 (無限等比級数を参照)
(無限等比級数を参照)