東京工業大学2003年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1](1) 3次関数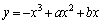
(
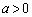)のグラフをCとする。原点を通る直線で、Cとちょうど2点を共有するものを2本求めよ。
(2) (1)で求めた直線のうち、傾きの大きい方を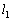
，小さい方を
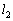とする。Cと
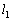が囲む部分の面積を
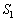，Cと
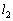が囲む部分の面積を
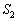とおく。この二つの面積の比
：
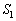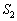を求めよ。 [解答へ]
[2] 2辺の長さの比が1：a (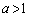
)の長方形がある。この長方形から1本の線分にそって切ることにより正方形を取り去る。残った図形が正方形でなければ、再び同じ要領で正方形を取り去り、残りが正方形でない限りこの操作を続ける。例えば、
，
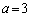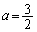の場合はどちらも2回でこの操作は終わる。
(1) 3回の操作で終わるようなaの値をすべて求めよ。
(2) n回の操作で終わるようなaの値の最大値と最小値を求めよ。
[解答へ]
[3]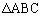 
において、辺ABの中点をM，辺ACの中点をNとする。辺ABをx：
(
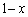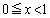)の比に内分する点Pと、辺ACをy：
(
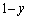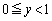)の比に内分する点Qをとり、線分BQと線分CPの交点をRとする。このとき、Rが
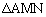に含まれるような
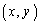の全体をxy平面に図示し、その面積を求めよ。(ただし、辺AB，辺ACを0：1の比に内分する点とは、ともに点Aのこととする。)
[解答へ]
[4] 関数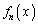
(
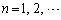)を次の漸化式により定める。
， 
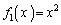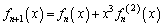
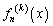は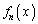
の第k次導関数を表す。
(1) 
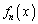は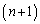
次多項式であることを示し、
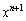の係数を求めよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東工大数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
，
，
，
を求めよ。