���H�吔�w'03�N�O��[4]
��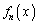 (
(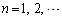 )�����̑Q�����ɂ���߂�B
)�����̑Q�����ɂ���߂�B
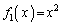 �C�@
�C�@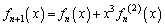
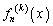 ��
��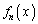 �̑�k��������\���B
�̑�k��������\���B
(1) 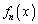 ��
��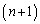 ���������ł��邱�Ƃ������A
���������ł��邱�Ƃ������A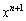 �̌W�������߂�B
�̌W�������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@������������o�Ă��܂����A���w�I�A�[�@�̖��ł��B(2)�̂��Ƃ����ɓ���āA�A�[�@�̏ؖ����l����Ƃ悢�ł��傤�B
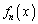 �̕��͋C�����ނ��߂ɁA
�̕��͋C�����ނ��߂ɁA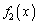 �C
�C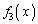 �C
�C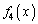 �����߂Ă݂܂��B
�����߂Ă݂܂��B
�^�Q�����ɂ����āA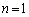 �Ƃ���ƁA
�Ƃ���ƁA
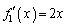 �C
�C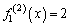 ���A
���A
�^�Q�����ɂ����āA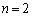 �Ƃ���ƁA
�Ƃ���ƁA
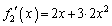 �C
�C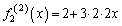 ���A
���A
�^�Q�����ɂ����āA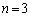 �Ƃ���ƁA
�Ƃ���ƁA
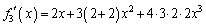 �C
�C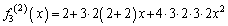 ���A
���A
����ŁA���̖��̑�̂̌����͂��Ă��܂��܂��B
(1) ��L�̌����ŁA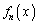 ��
��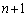 �����ɂȂ肻���Ȃ��Ƃ͏[���\���ł��܂��B
�����ɂȂ肻���Ȃ��Ƃ͏[���\���ł��܂��B �ō����̍�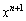 �̌W���ł����A
�̌W���ł����A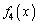 ��
��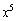 �̌W���F
�̌W���F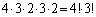 �ł����������܂����A�s���Ȃ�A
�ł����������܂����A�s���Ȃ�A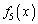 �̍ō����̍����l���Ă݂܂��傤�B
�̍ō����̍����l���Ă݂܂��傤�B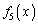 ��
��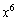 �̌W���́A
�̌W���́A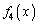 ��
��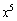 �̍���2���������
�̍���2���������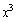 �����������̂ɂȂ�܂��B2���������ƁA�W����
�����������̂ɂȂ�܂��B2���������ƁA�W����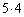 ���悶����̂ŁA
���悶����̂ŁA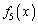 ��
��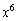 �̌W���́A
�̌W���́A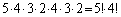 �ƂȂ�A
�ƂȂ�A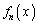 ��
��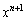 �̌W���́A
�̌W���́A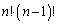 �Ɨ\���ł��܂��B(1)�Ƃ��āA���̗\�����ؖ�����悢�̂ł����A(2)�̂��Ƃ��l���Ă����܂��B��̐S�z������]�T���Ȃ������m��܂��A���̖��ł́A(2)���l���Ă���(1)�ɖ߂��čl�������Ă��A�[���A�������ԓ��ɓ���Ǝv���܂��B(2)�ł́A�����W�����Ă���̂ł����A1���A2���A3���A4���̔����W�������߂�ƌ����Ă���̂ŁA
�Ɨ\���ł��܂��B(1)�Ƃ��āA���̗\�����ؖ�����悢�̂ł����A(2)�̂��Ƃ��l���Ă����܂��B��̐S�z������]�T���Ȃ������m��܂��A���̖��ł́A(2)���l���Ă���(1)�ɖ߂��čl�������Ă��A�[���A�������ԓ��ɓ���Ǝv���܂��B(2)�ł́A�����W�����Ă���̂ł����A1���A2���A3���A4���̔����W�������߂�ƌ����Ă���̂ŁA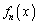 ��1���A2���A3���A4���̍��̌W�������ɂȂ肻���ł��B
��1���A2���A3���A4���̍��̌W�������ɂȂ肻���ł��B
��L�̌����ł����C�������Ƃł����A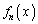 �ɂ́A�萔����1���̍����Ȃ����Ƃ��\���ł��܂��B������A���킹�āA�ؖ����Ă������Ƃɂ��܂��B�܂��A
�ɂ́A�萔����1���̍����Ȃ����Ƃ��\���ł��܂��B������A���킹�āA�ؖ����Ă������Ƃɂ��܂��B�܂��A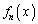 ��
��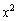 �C
�C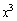 �C
�C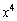 �̌W����
�̌W����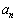 �C
�C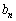 �C
�C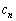 �Ƃ����܂�(
�Ƃ����܂�(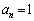 �C
�C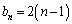 �ƂȂ邱�Ƃ��킩�肫���Ă��܂���)�B
�ƂȂ邱�Ƃ��킩�肫���Ă��܂���)�B
����F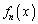 (
(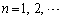 )�́A
)�́A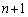 �����ł����āA
�����ł����āA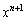 �̌W����
�̌W����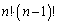 �ł���A
�ł���A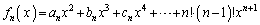 �Ƃ�����B
�Ƃ�����B
���̖�������w�I�A�[�@�ɂ��ؖ����܂��B (�T) 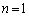 �̂Ƃ��A
�̂Ƃ��A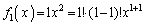 ���A
���A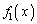 ��
��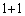 �����ł����āA
�����ł����āA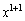 �̌W����
�̌W����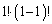 �ł���A
�ł���A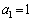 �C
�C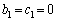 �Ƃ���A����͐������܂��B
�Ƃ���A����͐������܂��B (�U) 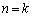 �̂Ƃ����肪��������Ƃ��āA
�̂Ƃ����肪��������Ƃ��āA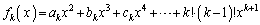 �Ƃ������Ƃ��܂��B
�Ƃ������Ƃ��܂��B �^�Q�����ɂ����āA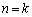 �Ƃ��āA
�Ƃ��āA 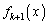 �́A
�́A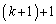 �����ł����āA
�����ł����āA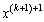 �̌W���́A
�̌W���́A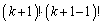 �ł���A
�ł���A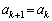 �C
�C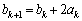 �C
�C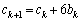 �Ƃ���A
�Ƃ���A
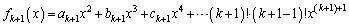 �Ƃ�����̂ŁA
�Ƃ�����̂ŁA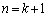 �̂Ƃ��ɂ�����͐������܂��B
�̂Ƃ��ɂ�����͐������܂��B(�T)�C(�U)���A���肪�ؖ�����܂����B
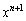 �̌W����
�̌W����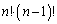 ......[��]
......[��]
(2) (1)�̏ؖ����A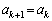 �C
�C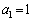 ���A
���A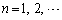 �ɑ��āA
�ɑ��āA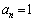 �ł��B
�ł��B 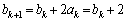 �C
�C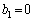 ���A����
���A����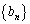 �́A����0�C����2�����������ł��B
�́A����0�C����2�����������ł��B
����āA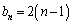
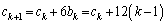 �C
�C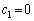 ���A
���A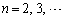 �Ƃ��āA
�Ƃ��āA�ȏ���A
��蕶���ɑQ�������^�����Ă��āA���̑Q������p���Đ��w�I�A�[�@�̏ؖ����\������ؖ����ŁA�ꐶ�����A�Q�������ؖ����悤�Ƃ���l�������̂ł����A�Q�����͐��藧�Ƃ���Ă���u�����v�ł��B���藧�Ƃ���Ă���u�����v�̏ؖ������݂Ă����̈Ӗ�������܂���B�����ؖ����ׂ��Ȃ̂��A�������炩�ɂ���Ă��Ȃ��̂��A�Ƃ������Ƃ��悭�l����悤�ɂ��Ă��������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B