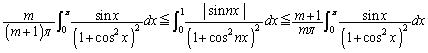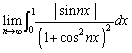東京工業大学2004年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] a,bを正の実数とする。
(1) 区間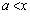 における関数
における関数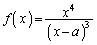 の増減を調べよ。
の増減を調べよ。 (2) 区間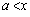 における関数
における関数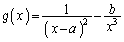 のグラフと相異なる3点で交わるx軸に平行な直線が存在するための必要十分条件を求めよ。
のグラフと相異なる3点で交わるx軸に平行な直線が存在するための必要十分条件を求めよ。 [解答へ]
[2] 次の問いに答えよ。
(1) 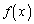 ,
,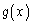 を連続な偶関数、mを正の整数とするとき、
を連続な偶関数、mを正の整数とするとき、 を証明せよ。
(2) 正の整数m,nが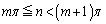 を満たしているとき、
を満たしているとき、 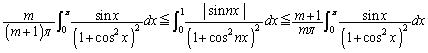 を証明せよ。
を証明せよ。(3) 極限値
を求めよ。
[解答へ]
[3] 3枚のコインP,Q,Rがある。P,Q,Rの表の出る確率をそれぞれp,q,rとする。このとき次の操作をn回繰り返す。まず、Pを投げて表が出ればQを、裏が出ればRを選ぶ。次にその選んだコインを投げて、表が出れば赤玉を、裏が出れば白玉をつぼの中に入れる。
(1) n回ともコインQを選び、つぼの中にはk個の赤玉が入っている確率を求めよ。
(2) つぼの中が赤玉だけとなる確率を求めよ。
(3) 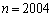 ,
,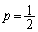 ,
,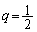 ,
,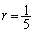 のとき、つぼの中に何個の赤玉が入っていることがもっとも起こりやすいかを求めよ。
のとき、つぼの中に何個の赤玉が入っていることがもっとも起こりやすいかを求めよ。 [解答へ]
[4] 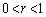 とする。空間において、点
とする。空間において、点 を中心とする半径rの球と点
を中心とする半径rの球と点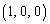 を中心とする半径
を中心とする半径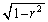 の球との共通部分の体積を
の球との共通部分の体積を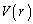 とする。次の問に答えよ。
とする。次の問に答えよ。
(1) 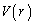 を求めよ。
を求めよ。 (2) rが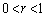 の範囲を動くとき、
の範囲を動くとき、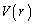 を最大にするrの値及び
を最大にするrの値及び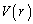 の最大値を求めよ。
の最大値を求めよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東工大数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。