���H�吔�w'04�N�O��[2]
���̖₢�ɓ�����B
(1) 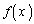 �C
�C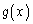 ��A���ȋ���Am�𐳂̐����Ƃ���Ƃ��A
��A���ȋ���Am�𐳂̐����Ƃ���Ƃ��A ���ؖ�����B
(2) ���̐���m�Cn��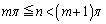 �����Ă���Ƃ��A
�����Ă���Ƃ��A 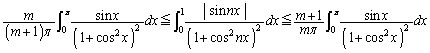 ���ؖ�����B
���ؖ�����B(3) �Ɍ��l
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�͐ϕ���Ԃ��邱�Ƃɂ��A��������Ɖ������܂��B(2)�́A��ϕ����̌`���悭���āA(1)�𗘗p���邱�Ƃ��l���܂��B(3)�́A�͂��݂����̌������g�����H��ŕp�o�^�C�v�̖��ł��B�Ȃ��A�O�p���A�O�p���̃O���t�A���E����̐ϕ����Q�Ƃ��Ă��������B
(1) 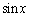 �C
�C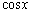 �͎���
�͎���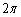 �̎�����(�O�p���̃O���t���Q��)�ŁA
�̎�����(�O�p���̃O���t���Q��)�ŁA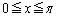 ��
��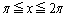 �Ƃɂ����ẮA���̒l�͐������قȂ邾���ł��B
�Ƃɂ����ẮA���̒l�͐������قȂ邾���ł��B ���ŏ����ƁA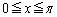 �̂Ƃ��A
�̂Ƃ��A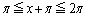 �ł����āA
�ł����āA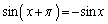 �C
�C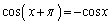
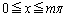 �͈̔͂̐ϕ��́A
�͈̔͂̐ϕ��́A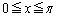 �C
�C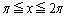 �C����C
�C����C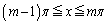 �Ɣ͈͂��Đϕ����܂��B
�Ɣ͈͂��Đϕ����܂��B k��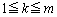 ���������Ƃ��āA
���������Ƃ��āA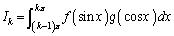 �Ƃ����ƁA
�Ƃ����ƁA �����ŁA�u���ϕ����s���āA�ϕ�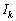 ��
��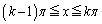 �Ƃ����ϕ��͈͂�
�Ƃ����ϕ��͈͂�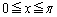 �ɂ��邱�Ƃ��l���܂��B
�ɂ��邱�Ƃ��l���܂��B
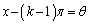 �Ƃ����ƁA
�Ƃ����ƁA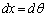 �Cx�F
�Cx�F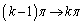 �̂Ƃ��A?�F
�̂Ƃ��A?�F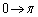
k�������̂Ƃ��A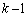 �͊�ł����āA
�͊�ł����āA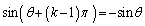 �C
�C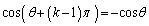 k����̂Ƃ��A
k����̂Ƃ��A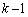 �͋����ł����āA
�͋����ł����āA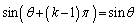 �C
�C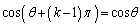
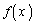 �͋��������A�C�ӂ̎���x�ɑ��āA
�͋��������A�C�ӂ̎���x�ɑ��āA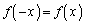 �����藧���܂��B
�����藧���܂��B
�]���āA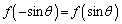 �C
�C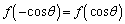 �����藧���܂��B
�����藧���܂��B
����āAk������������ɂ�����炸�A 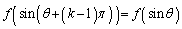 �C
�C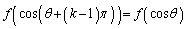
�����藧���܂��B
�� 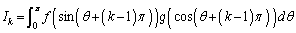
�܂�A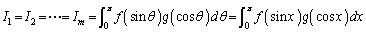
�� 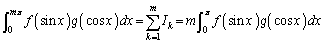 �@(�ؖ��I)
�@(�ؖ��I)
(2) �܂��A�ؖ����ׂ��s�����ɂ����āA�s�����̕s�����ɋ��܂ꂽ�����̐ϕ��̌`�����ӁA�E�ӂ̐ϕ��Ɠ����悤�Ȍ`�ɂ��邱�Ƃ��l���܂��B
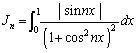 �ɂ����āA
�ɂ����āA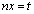 �Ƃ����ƁA
�Ƃ����ƁA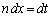 �Cx�F
�Cx�F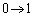 �̂Ƃ�t�F
�̂Ƃ�t�F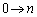
�� 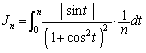 (�u���ϕ��Q��)
(�u���ϕ��Q��)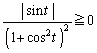 �C
�C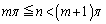 ���A
���A�e�ӂ�n�Ŋ���A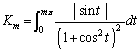 �Ƃ����ƁA
�Ƃ����ƁA 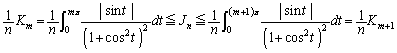 �@����@
�@����@����ɁA�@�̍��ӂ́A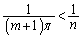 ���A
���A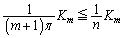
�@�̉E�ӂ́A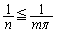 ���A
���A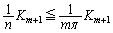
�� 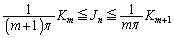 ����A
����A
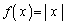 �C
�C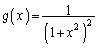 �Ƃ��܂��B����
�Ƃ��܂��B����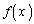 �C
�C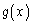 �́A
�́A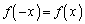 �C
�C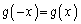 �����̂ŁA���ꂼ�����ł��B
�����̂ŁA���ꂼ�����ł��B
�]���āA(1)�𗘗p���āA �E�ӂɏo�Ă���ϕ��́A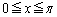 �ɂ����ẮA
�ɂ����ẮA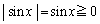 ������A
������A 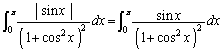 ����B
����B�A���A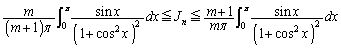 �@(�ؖ��I)
�@(�ؖ��I)
(3) �B�̐ϕ��ŁA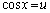 �Ƃ����ƁA
�Ƃ����ƁA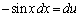 �Cx�F
�Cx�F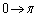 �̂Ƃ��Au�F
�̂Ƃ��Au�F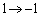
����ɁA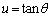 �Ƃ����ƁA
�Ƃ����ƁA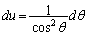 �Cu�F
�Cu�F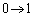 �̂Ƃ��A?�F
�̂Ƃ��A?�F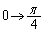
�����p����ƁA(2)�̕s�������A
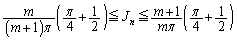 ����C
����C�����ŁA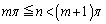 ���
���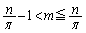 �C
�C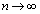 �Ƃ���ƁA�͂��݂����̌������A
�Ƃ���ƁA�͂��݂����̌������A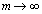
���̂Ƃ��A�C�ɂ����āA����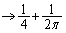 �C�E��
�C�E��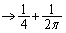 �ƂȂ邩��A�͂��݂����̌������A
�ƂȂ邩��A�͂��݂����̌������A 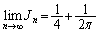 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 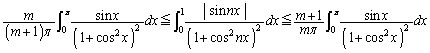
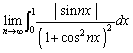
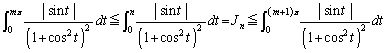
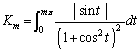 �Ƃ����ƁA
�Ƃ����ƁA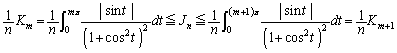 �@����@
�@����@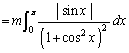
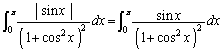 ����B
����B