���H�吔�w'05�N�O��[1]
e�����R�ΐ��̒�Ƃ��A����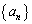 �������Œ�`����B
�������Œ�`����B
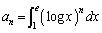 (
( )
)(1) 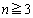 �̂Ƃ��A���̑Q�����������B
�̂Ƃ��A���̑Q�����������B (2) 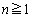 �ɑ�
�ɑ� �Ȃ邱�Ƃ������B
�Ȃ邱�Ƃ������B (3)  �̂Ƃ��A�ȉ��̕s�������������邱�Ƃ������B
�̂Ƃ��A�ȉ��̕s�������������邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���̃^�C�v�̖��ł́A���ʂ������ϕ��ɂ���đQ�������܂��B
���̖��ł������ϕ����邱�Ƃ��l���܂��B
��ϕ���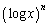 �́A
�́A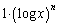 �ƌ��āA1��
�ƌ��āA1�� �Ƃ��ĕ����ϕ����s���܂��B
�Ƃ��ĕ����ϕ����s���܂��B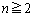 �̂Ƃ��A
�̂Ƃ��A �� 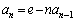 ����@�@(
����@�@(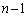 �Ƃ����ԍ����o�Ă���̂ŁA
�Ƃ����ԍ����o�Ă���̂ŁA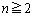 �Ƃ�������������K�v������܂��B)�ԍ���1���炵�āA
�Ƃ�������������K�v������܂��B)�ԍ���1���炵�āA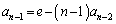 ����A�@(
����A�@(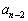 �̌W����n�łȂ��A
�̌W����n�łȂ��A �ƂȂ邱�Ƃɒ��ӂ��邱�ƁB�܂��A
�ƂȂ邱�Ƃɒ��ӂ��邱�ƁB�܂��A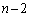 �Ƃ����ԍ����o�Ă���̂ŁA
�Ƃ����ԍ����o�Ă���̂ŁA �Ƃ�������������K�v������܂�)�@�|�A���A
�Ƃ�������������K�v������܂�)�@�|�A���A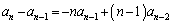 (
( )��
)�� 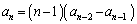 (
(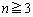 )
)
(2) �� �́A
�́A �ɂ����āA
�ɂ����āA �ł̂�
�ł̂�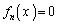 �ŁA
�ŁA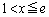 �ɂ����Ă�
�ɂ����Ă�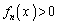 �C����āA
�C����āA 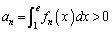 (
( )
)�܂��A �ɂ����Ă̂�
�ɂ����Ă̂� (
( �C
�C )�ł���A
)�ł���A
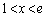 �ɂ�����
�ɂ����� ���A
���A
(3) (1)��(2)�Ƃ���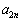 ��
��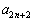 �Ɋւ���W����������w�I�A�[�@�Ƃ����X�g�[���[�ɂȂ邾�낤�ƌ��������܂��B
�Ɋւ���W����������w�I�A�[�@�Ƃ����X�g�[���[�ɂȂ邾�낤�ƌ��������܂��B 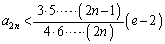 ���Ƃ���ƁA
���Ƃ���ƁA�̂悤�ɂȂ�̂ŁA
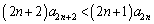 �Ƃ����`�̕s��������邱�Ƃ�ڕW�ɂ��܂��B
�Ƃ����`�̕s��������邱�Ƃ�ڕW�ɂ��܂��B
�܂��A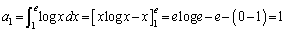 �@(�s��ϕ��̌������Q��)
�@(�s��ϕ��̌������Q��)
(1)�̌��ʂɂ�����n�� �ɒu��������ƁA
�ɒu��������ƁA  (
(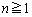 ) ����B
) ����B ��
�� �̊W�ׂ邱�ƂɂȂ�܂����A�B��
�̊W�ׂ邱�ƂɂȂ�܂����A�B�� ���ז��ɂȂ�܂��B
���ז��ɂȂ�܂��B
������������߂ɁA(2)��n��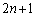 �ɒu�������āA
�ɒu�������āA �C�]���āA
�C�]���āA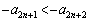
�B�ɓK�p����ƁA�� 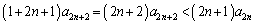 ����C
����C
�C��p���āA���w�I�A�[�@�ɂ��^�s�����������܂��B(�T)  �̂Ƃ��A�@��p���āA
�̂Ƃ��A�@��p���āA 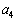 ��
��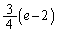 �̑召�W���ׂ�悢�̂ł����A
�̑召�W���ׂ�悢�̂ł����A1���������F �������ƁA
�������ƁA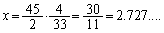 �Ȃ̂ŁA
�Ȃ̂ŁA
 �������Ƃ��āA�Ⴆ�A
�������Ƃ��āA�Ⴆ�A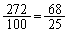 �������Ă���ƁA
�������Ă���ƁA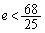 �ł����āA
�ł����āA ��  ��
�� 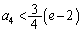 ����āA
����āA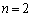 �̂Ƃ��A�^�s���������藧���܂��B(�U)
�̂Ƃ��A�^�s���������藧���܂��B(�U) 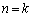 �̂Ƃ��A�^�s���������藧�Ɖ��肷��B���̂Ƃ��A
�̂Ƃ��A�^�s���������藧�Ɖ��肷��B���̂Ƃ��A �����藧���܂��B
�C���A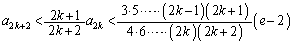
����āA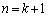 �̂Ƃ����A�^�s���������藧���܂��B(�T)�C(�U)���A
�̂Ƃ����A�^�s���������藧���܂��B(�T)�C(�U)���A �̂Ƃ��A�^�s���������藧���܂��B
�̂Ƃ��A�^�s���������藧���܂��B
���D���ǁA�C���J��Ԃ��p����A �ƂȂ��Ă��܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B