���H�吔�w'05�N�O��[4]
����x�Cy��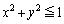 �����Ȃ���ω�����Ƃ���B
�����Ȃ���ω�����Ƃ���B
(1) 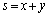 �C
�C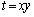 �Ƃ���Ƃ��A�_
�Ƃ���Ƃ��A�_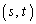 �̓����͈͂�st���ʏ�ɐ}������B
�̓����͈͂�st���ʏ�ɐ}������B (2) ���łȂ��萔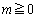 ���Ƃ�Ƃ��A
���Ƃ�Ƃ��A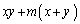 �̍ő�l�A�ŏ��l��m��p���ĕ\���B
�̍ő�l�A�ŏ��l��m��p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@2�����̘a�Ɛς��������ł͒��ӂ��K�v�ł��B���̖��ł������Ȃ̂ł����As�Ct��2����x�Cy�̘a�ƐςɂȂ��Ă���Ƃ��������Ŗ����I�ɂ͌���Ă��Ȃ��B�ꂽ����������܂��B�hx�Cy�������ł����h�Ƃ��������͌����������Ȃ̂ł��Bx�Cy���݂��ɋ����ȕ��f���ŋ����̂Ƃ��A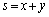 ��
��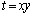 �������ɂȂ�܂����Ax�Cy�͎����ł͂���܂���B
�������ɂȂ�܂����Ax�Cy�͎����ł͂���܂���B
(1) x�Cy�������A�Ƃ����������������߂ɁAx�Cy��2���Ƃ���2���������F 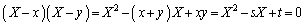 ����@
����@���l���܂��B2��x�Cy�͎����Ȃ̂ŁA�@�̔��ʎ��F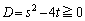
�� 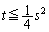 ����A
����A
���̇A�̏����́A��蕶�̒��ŁA�u����̂��߂̏����v�Ƃ������ɏ�����Ă���킯�ł͂Ȃ��̂ŁA2�����̘a�Ɛς��o�Ă����i�K�ŁA2���������̔��ʎ����`�F�b�N����K�v���������Ƃ��o���Ă����Ȃ��Ƃ����܂���B
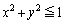 ���A
���A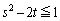
�� 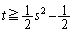 ����B
����B
�A�C�B�̋��E���́A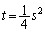 ����C�C
����C�C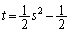 ����D
����D�C�C�D��A�����Č�_�����߂Ă����܂��B
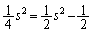 �C
�C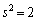
�� 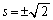 �C���̂Ƃ��A
�C���̂Ƃ��A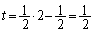
����āA�C�C�D�̌�_�́A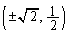
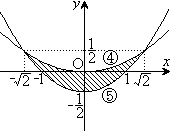 ���߂�̈�́A�������C���牺�ŁA�������D�����ł��B
���߂�̈�́A�������C���牺�ŁA�������D�����ł��B
�}������ƁA�E�}�ΐ���(���E�����܂�)�ɂȂ�܂��B
�������ł����A�B�����ł͌듚�ɂȂ�܂��B2����������2���������������F�A���������K�v������܂��B
(2) 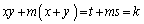 �Ƃ����ƁA
�Ƃ����ƁA �́Ast���ʏ�ŁA�X���F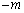 (
(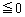 )�Ct�ؕЁFk�̒���l��\���܂��B
)�Ct�ؕЁFk�̒���l��\���܂��B
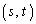 ��(1)�ŋ��߂��̈���ɑ��݂���̂ŁA����l��(1)�̗̈�Ƌ��L�_�������܂��B�X�����̒�����(1)�̃O���t��ŃX���C�h�����Ă݂Ă��������B(1)�̗̈�́A
��(1)�ŋ��߂��̈���ɑ��݂���̂ŁA����l��(1)�̗̈�Ƌ��L�_�������܂��B�X�����̒�����(1)�̃O���t��ŃX���C�h�����Ă݂Ă��������B(1)�̗̈�́A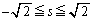 �͈̔͂ɑ��݂���̂ŁA����l��(1)�̗̈�Ƌ��L�_�����Ƃ��At�ؕ�k���ŏ��ɂȂ�̂́A����l���_
�͈̔͂ɑ��݂���̂ŁA����l��(1)�̗̈�Ƌ��L�_�����Ƃ��At�ؕ�k���ŏ��ɂȂ�̂́A����l���_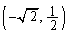 ��ʂ�Ƃ��ƁA�������A�ɐڂ���ꍇ�Ƃɕ������܂��B
��ʂ�Ƃ��ƁA�������A�ɐڂ���ꍇ�Ƃɕ������܂��B
�E����l���������D��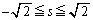 �̕����Őڂ���Ƃ��A�D�̓����F
�̕����Őڂ���Ƃ��A�D�̓����F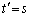
�ڐ��̌X����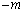 �ɂȂ�̂́A
�ɂȂ�̂́A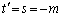 �̂Ƃ��ŁA
�̂Ƃ��ŁA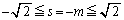 ��
��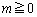 ���A
���A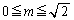
���̂Ƃ��A 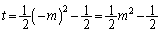 �C
�C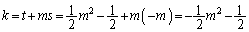
����k�̒l���ŏ��l�ɂȂ�܂��B
�E����l��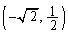 ��ʂ�Ƃ��A
��ʂ�Ƃ��A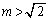
����k�̒l���ŏ��l�ɂȂ�܂��B
����l��(1)�̗̈�Ƌ��L�_�����Ƃ��At�ؕ�k���ő�ɂȂ�̂́A����l��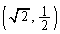 ��ʂ�Ƃ��ł��B���̂Ƃ��A
��ʂ�Ƃ��ł��B���̂Ƃ��A �ȏ���A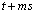 �́A
�́A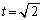 �C
�C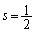 �̂Ƃ��A�ő�l�F
�̂Ƃ��A�ő�l�F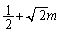 .......[��]
.......[��] �E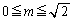 �̂Ƃ��A
�̂Ƃ��A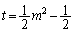 �C
�C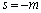 �̂Ƃ��A�ŏ��l�F
�̂Ƃ��A�ŏ��l�F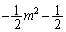 ......[��]
......[��] �E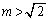 �̂Ƃ��A
�̂Ƃ��A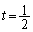 �C
�C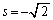 �̂Ƃ��A�ŏ��l�F
�̂Ƃ��A�ŏ��l�F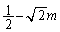 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B