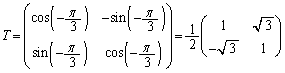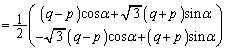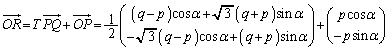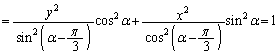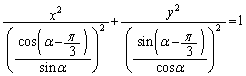���H�吔�w'08�N�O��[4]
���ʂ̌��_O��[�_�Ƃ��Ax���ƂȂ��p�����ꂼ��A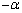 �Cα (������
�Cα (������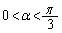 )�ł��锼������
)�ł��锼������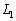 �C
�C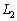 �Ƃ���B
�Ƃ���B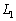 ��ɓ_P�C
��ɓ_P�C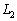 ��ɓ_Q�����PQ�̒�����1�ƂȂ�悤�ɂƂ�A�_R���A����PQ�ɑ����_O�̔��Α��Ɂ�PQR�����O�p�`�ɂȂ�悤�ɂƂ�B
��ɓ_Q�����PQ�̒�����1�ƂȂ�悤�ɂƂ�A�_R���A����PQ�ɑ����_O�̔��Α��Ɂ�PQR�����O�p�`�ɂȂ�悤�ɂƂ�B
(1) ����PQ��x���ƒ�������Ƃ��A�_R�̍��W�����߂�B
(2) 2�_P�CQ���A����PQ�̒�����1�ɕۂ����܂�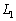 �C
�C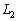 ����Ƃ��A�_R�̋O�Ղ͂���ȉ~�̈ꕔ�ł��邱�Ƃ������B
����Ƃ��A�_R�̋O�Ղ͂���ȉ~�̈ꕔ�ł��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��]�ړ��ɂ��ẮA1���ϊ����Q�Ƃ��Ă��������B
(1) PQ��x���Ƃ̌�_(PQ�̒��_)��M�Ƃ��܂��B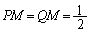 �ł��B
�ł��B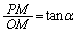 ���A
���A ���̂Ƃ��AR��x����̓_�ŁA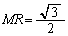
�� 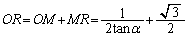
R�̍��W�́A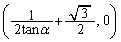
(2) 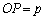 �C
�C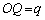 �Ƃ���ƁAP�CQ�̍��W�́A
�Ƃ���ƁAP�CQ�̍��W�́A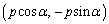 �C
�C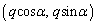
�܂��A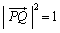 ���(�������Q��)�A
���(�������Q��)�A 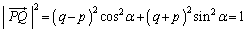 �@����@
�@����@�_Q��_P�̂܂���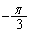 ��]����Ɠ_R�ɗ��܂��B
��]����Ɠ_R�ɗ��܂��B
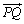 �����_�̂܂���
�����_�̂܂���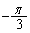 ��]����ƁA
��]����ƁA ���A
������A�n�_�����_����_P�ɂ���悤�ɕ��s�ړ�����ƁA�I�_���_R�ɗ��܂��B
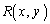 �Ƃ��āA
�Ƃ��āA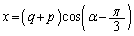 �C
�C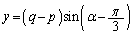
�@����p���āAp�Cq����������ƁA
�� 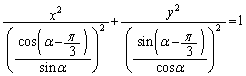
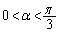 ���A
���A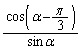 �C
�C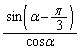 �́A0�ł͂Ȃ��L���Ȓl�̒萔�Ȃ̂ŁAR
�́A0�ł͂Ȃ��L���Ȓl�̒萔�Ȃ̂ŁAR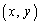 �̋O�Ղ��ȉ~�̈ꕔ�ł��B
�̋O�Ղ��ȉ~�̈ꕔ�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B