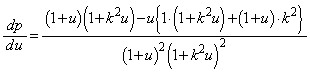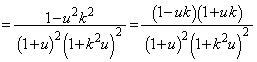���H�吔�w'11�N�O��[3]
�萔k��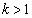 ���݂����Ƃ���Bxy���ʏ�̓_A
���݂����Ƃ���Bxy���ʏ�̓_A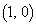 ��ʂ�x���ɐ����Ȓ����̑�1�ی��Ɋ܂܂�镔�����A2�_X�CY��
��ʂ�x���ɐ����Ȓ����̑�1�ی��Ɋ܂܂�镔�����A2�_X�CY��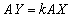 ���݂����Ȃ��瓮���Ă���B���_O
���݂����Ȃ��瓮���Ă���B���_O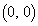 �𒆐S�Ƃ��锼�a1�̉~�Ɛ���OX�COY�������_�����ꂼ��P�CQ�Ƃ���Ƃ��A��OPQ�̖ʐς̍ő�l��k��p���ĕ\���B
�𒆐S�Ƃ��锼�a1�̉~�Ɛ���OX�COY�������_�����ꂼ��P�CQ�Ƃ���Ƃ��A��OPQ�̖ʐς̍ő�l��k��p���ĕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ŏI�I�� �̌`���o�Ă��܂����A2���������̉��̔z�u���l���邱�Ƃɂ��ő�l�����߂邱�Ƃ��ł��܂��B
�̌`���o�Ă��܂����A2���������̉��̔z�u���l���邱�Ƃɂ��ő�l�����߂邱�Ƃ��ł��܂��B
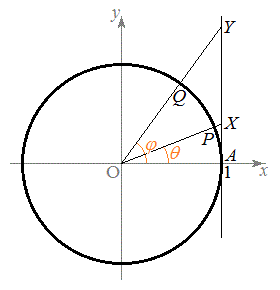
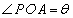 �C
�C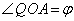 �Ƃ���ƁA
�Ƃ���ƁA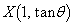 �CY
�CY
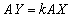 ���A
���A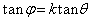 �@����@
�@����@
X�CY�͑�1�ی��̓_�Ȃ̂�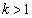 ���A
���A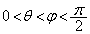
�܂��A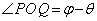 �ŁA��OPQ�̖ʐ�S�́A
�ŁA��OPQ�̖ʐ�S�́A
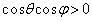 �Ƈ@���A
�Ƈ@���A
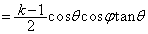 �@����A
�@����A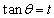 �Ƃ����ƁA
�Ƃ����ƁA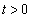 �ł����āA�@���A
�ł����āA�@���A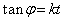
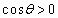 ���A
���A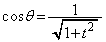
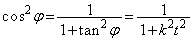 �@(�� �@)
�@(�� �@)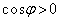 ���A
���A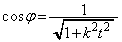
�������A�ɑ�����āA
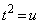 �Ƃ����ƁA
�Ƃ����ƁA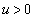 �ł����āA���������o���āA
�ł����āA���������o���āA
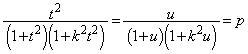 �@����B
�@����B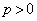 �ł��B������Đ�������ƁA
�ł��B������Đ�������ƁA
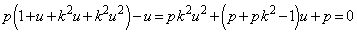 �@����C
�@����C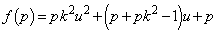 �Ƃ����ƁA
�Ƃ����ƁA
u��2���������C���A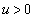 �͈̔͂Ɏ��������������́A
�͈̔͂Ɏ��������������́A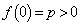 �Ȃ̂ŁA�C�̔��ʎ�D�C���ʒu�F
�Ȃ̂ŁA�C�̔��ʎ�D�C���ʒu�F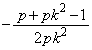 �ɂ��āA
�ɂ��āA
���ʎ��F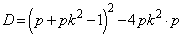
���ʒu�F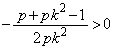 �@����E
�@����E �����ŁA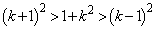 ���A
���A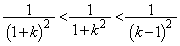 �ɒ��ӂ���ƁA
�ɒ��ӂ���ƁA
�D���A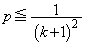 �C
�C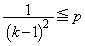
�E���A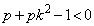 �C
�C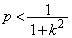
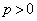 ���l�����āA
���l�����āA
�D ���� �E �� 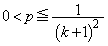
������AS�̍ő�l�́A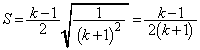 ......[��]
......[��]
���DS���ő�ƂȂ�̂́A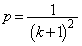 �̂Ƃ��ł����A���̂Ƃ��A�������C���d���F
�̂Ƃ��ł����A���̂Ƃ��A�������C���d���F �������A���̂Ƃ��A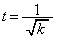 �ł��B
�ł��B �ʉ��D�B��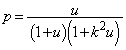 ��u�̊��ƌ��Ĕ�������ƁA
��u�̊��ƌ��Ĕ�������ƁA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 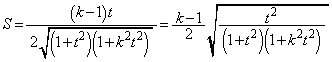
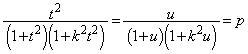 �@����B
�@����B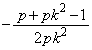 �ɂ��āA
�ɂ��āA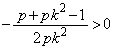 �@����E
�@����E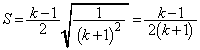 ......[��]
......[��]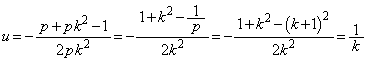
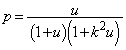 ��u�̊��ƌ��Ĕ�������ƁA
��u�̊��ƌ��Ĕ�������ƁA