���H�吔�w'13�N�O��[2]
2���̐����s��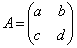 �ɑ��āA
�ɑ��āA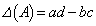 �C
�C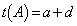 �ƒ�߂�B
�ƒ�߂�B
(1) 2���̐����s��A�CB�ɑ��āA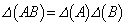 �����藧���Ƃ������B
�����藧���Ƃ������B (2) A�̐��������ׂĎ����ŁA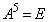 �����藧�Ƃ��A
�����藧�Ƃ��A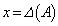 ��
��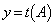 �̒l�����߂�B�������AE��2���̒P�ʍs��Ƃ���B
�̒l�����߂�B�������AE��2���̒P�ʍs��Ƃ���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�P�[���[��n�~���g���̒藝�𗘗p���Ď����������s�����ł��B
(1) 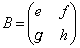 �Ƃ��܂��B
�Ƃ��܂��B
(2) (1)�𗘗p���āA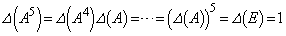
A�̐����͂��ׂĎ����Ȃ̂ŁA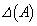 �������ł��B
�������ł��B
�� 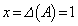 �@����@
�@����@
�P�[���[�E�n�~���g���̒藝���A 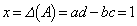 �C
�C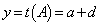 ���A
���A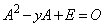
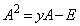 �@����A
�@����A�Ȍ�A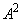 ���o�Ă��邽�тɁA
���o�Ă��邽�тɁA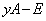 �Ɠ���ւ��܂��B
�Ɠ���ւ��܂��B �� 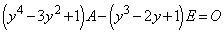 �@����B
�@����B ������A�B�́A
�� 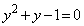 ����C �܂���
����C �܂��� 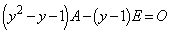 ����D
����D �E�C�̂Ƃ��A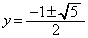 �@����E
�@����E �E�D�̂Ƃ��A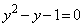 �Ȃ�
�Ȃ�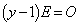 �ƂȂ�
�ƂȂ�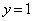 �ł����A
�ł����A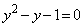 ��
��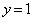 �͗������Ȃ��̂ŕs�K�B�]����
�͗������Ȃ��̂ŕs�K�B�]����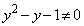 �ł����A
�ł����A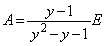 �ƂȂ�A
�ƂȂ�A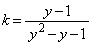 �@����F�@�Ƃ����A
�@����F�@�Ƃ����A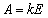 �̌`�ɏ����܂��B���̂Ƃ��́A
�̌`�ɏ����܂��B���̂Ƃ��́A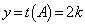 �ƂȂ�܂����A�F���A
�ƂȂ�܂����A�F���A �� 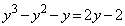
�� 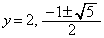 ���̂����A
���̂����A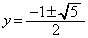 �C
�C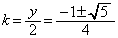 �ł́A
�ł́A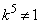 �ł����āA
�ł����āA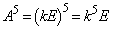 ��
��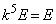 �ƂȂ�Ȃ�(
�ƂȂ�Ȃ�(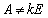 �̌`�ł���·E���
�̌`�ł���·E���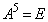 �ɂȂ�)�̂ŁA
�ɂȂ�)�̂ŁA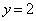 �@����G
�@����G �@�C�E�C�G���A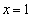 �C
�C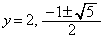 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B