東京工業大学2013年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1](1) 2次方程式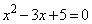
の2つの解α，β に対し、
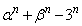はすべての正の整数nについて5の整数倍になることを示せ。 (2) 6個のさいころを同時に投げるとき、ちょうど4種類の目が出る確率を規約分数で表せ。
[解答へ]
(1) 2次の正方行列A，Bに対して、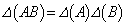
が成り立つことを示せ。 (2) Aの成分がすべて実数で、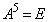
が成り立つとき、
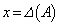と
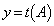の値を求めよ。ただし、Eは2次の単位行列とする。 [解答へ]
[3] kを定数とするとき、方程式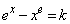
の異なる正の解の個数を求めよ。
[解答へ]
[4] 正の整数nに対し、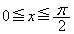
の範囲において
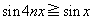を満たすxの区間の長さの総和を
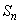とする。このとき、
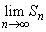を求めよ。
[解答へ]
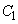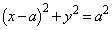[5] a，bを正の実数とし、円
：
と楕円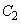
：
を考える。
(1) 
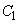が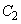
に内接するためのa，bの条件を求めよ。 (2) 
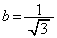とし、
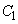が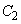
に内接しているとする。このとき、第1象限における
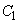と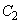
の接点の座標
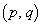を求めよ。 (3) (2)の条件のもとで、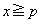
の範囲において、
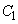と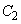
で囲まれた部分の面積を求めよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東工大数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
に対して、
，
と定める。