���H�吔�w'13�N�O��[1]
(1) 2��������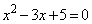 ��2�̉�α�Cβ �ɑ��A
��2�̉�α�Cβ �ɑ��A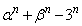 �͂��ׂĂ̐��̐���n�ɂ���5�̐����{�ɂȂ邱�Ƃ������B
�͂��ׂĂ̐��̐���n�ɂ���5�̐����{�ɂȂ邱�Ƃ������B (2) 6�̂���������ɓ�����Ƃ��A���傤��4��ނ̖ڂ��o��m�����K���ŕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�͗ޑ肪'86�N[1]�ɂ���܂��B(2)�͓���Ȃ��ł����A���J�ɏꍇ�̐��ׂ�K�v������܂��B
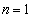 �̂Ƃ��A�@���A
�̂Ƃ��A�@���A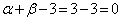 �C�����5�������{�ł����āA�^����ꂽ����͐��藧���܂��B
�C�����5�������{�ł����āA�^����ꂽ����͐��藧���܂��B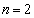 �̂Ƃ��A�@���A
�̂Ƃ��A�@���A�����5�̐����{�ł����āA�^����ꂽ����͐��藧���܂��B
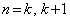 �̂Ƃ��A
�̂Ƃ��A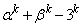 �C
�C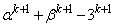 ��5�̐����{�ł���Ɖ��肵�܂��Bp�Cq�𐮐��Ƃ��āA
��5�̐����{�ł���Ɖ��肵�܂��Bp�Cq�𐮐��Ƃ��āA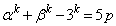 �C
�C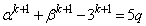 �@����A
�@����A�Ƃ����܂��B�@�C�A�𗘗p���āA
��5�̐����{�ł����āA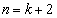 �̂Ƃ��ɂ��^����ꂽ����͐��藧���܂��B
�̂Ƃ��ɂ��^����ꂽ����͐��藧���܂��B �ȏ���A���w�I�A�[�@�ɂ��A���ׂĂ̐��̐���n�ɂ���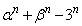 ��5�̐����{�ɂȂ�܂��B
��5�̐����{�ɂȂ�܂��B �ʉ��D3���ԑQ����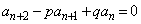 �̓�����������
�̓�����������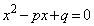 �ɂȂ邱�Ƃ𗘗p����A3���ԑQ�������l���邱�Ƃ��ł��܂��B
�ɂȂ邱�Ƃ𗘗p����A3���ԑQ�������l���邱�Ƃ��ł��܂��B 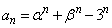 �Ƃ����ƁA
�Ƃ����ƁA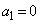 �C
�C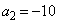 ��5�̐����{�ŁAp�Cq�𐮐��Ƃ��āA
��5�̐����{�ŁAp�Cq�𐮐��Ƃ��āA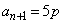 �C
�C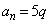 �ł���A
�ł���A
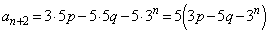 ��5�̔{���ł��B
��5�̔{���ł��B
(2) 6�̂�������𓊂���Ƃ��A�e�X�̖ڂ̏o���́A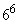 �ʂ肠��܂��B
�ʂ肠��܂��B ���傤��4��ނ̖ڂ��o��̂́A(i) 6�̂���3�������ڂŁA����3���݂��ɈقȂ�A���A�����ڂ�3�Ƃ��قȂ�B���A(ii) 6�̂���2�������ڂŁA2������Ƃ͈قȂ铯���ڂŁA����2������2��̖ڂƈقȂ�A���A�݂��ɈقȂ�ڂɂȂ�B�ꍇ�ł��B
(i)�̂Ƃ��A4��ނ̖ڂ̑I�ѕ���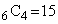 �ʂ�B6�̂��������ڂɂȂ�3�̑I�ѕ���
�ʂ�B6�̂��������ڂɂȂ�3�̑I�ѕ���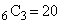 �ʂ�B4��ނ̖ڂ̕��ѕ����A
�ʂ�B4��ނ̖ڂ̕��ѕ����A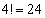 �ʂ�B
�ʂ�B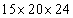 �ʂ肠��܂��B
�ʂ肠��܂��B (ii)�̂Ƃ��A4��ނ̖ڂ̑I�ѕ���15�ʂ�B6�̂��������ڂɂȂ�2�g��2�̂�������̑I�ѕ����A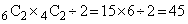 �ʂ�(2�g�͋�ʂł��Ȃ�)�B4��ނ̖ڂ̕��ѕ���24�ʂ�B
�ʂ�(2�g�͋�ʂł��Ȃ�)�B4��ނ̖ڂ̕��ѕ���24�ʂ�B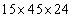 �ʂ肠��܂��B
�ʂ肠��܂��B 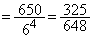 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B