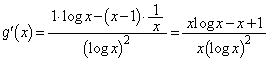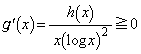���H�吔�w'13�N�O��[3]
k��萔�Ƃ���Ƃ��A������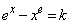 �̈قȂ鐳�̉��̌������߂�B
�̈قȂ鐳�̉��̌������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@������ŔM���Ȃ��Ă��܂��ƋC�Â��ɂ����ł����A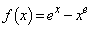 �Ƃ����ƁA
�Ƃ����ƁA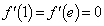 �ł��B�Ƃ肠�����A���̕��͋C�����ނ��߂ɂ��A�ȒP�Ȑ��l�������Ă݂�A�Ƃ����S����������Ƃ������Ƃł��傤�B
�ł��B�Ƃ肠�����A���̕��͋C�����ނ��߂ɂ��A�ȒP�Ȑ��l�������Ă݂�A�Ƃ����S����������Ƃ������Ƃł��傤�B
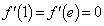 �ƂȂ�܂����A����ȊO��
�ƂȂ�܂����A����ȊO��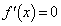 �ƂȂ�x�����邩�ǂ������ׂ܂��B
�ƂȂ�x�����邩�ǂ������ׂ܂��B
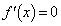 �Ƃ���ƁA
�Ƃ���ƁA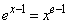
���ӂ̑ΐ�(��Fe)���Ƃ�A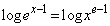
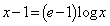 �@����@
�@����@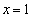 �̂Ƃ��A�@�͐������A
�̂Ƃ��A�@�͐������A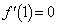 �@����A
�@����A
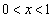 �C
�C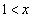 �ɂ����ẮA�@���A
�ɂ����ẮA�@���A
�Ƃ����܂��B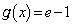 ����x��
����x��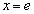 �ȊO�ɂ��邩�ǂ������ׂ܂��B
�ȊO�ɂ��邩�ǂ������ׂ܂��B
������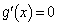 �Ƃ��Ă݂Ă����������Ȃ��̂ŁA���̕��q��
�Ƃ��Ă݂Ă����������Ȃ��̂ŁA���̕��q��
�Ƃ����āA����ɒ��ׂ܂��B
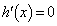 �Ƃ���ƁA
�Ƃ���ƁA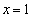
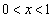 �ɂ�����
�ɂ�����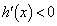 ���
���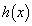 �����C
�����C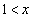 �ɂ�����
�ɂ�����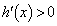 ���
���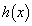 ����(���̑������Q��)�C����āA
����(���̑������Q��)�C����āA
����āA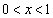 �C
�C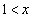 �ɂ�����
�ɂ�����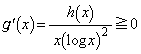
������A �́A
�́A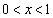 �C
�C �ɂ����đ������ŁA
�ɂ����đ������ŁA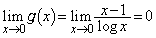 �C
�C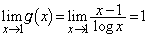 (�Ɍ��̌������Q��)�C
(�Ɍ��̌������Q��)�C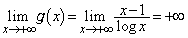
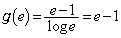 �ł����A����ȊO�ɁA
�ł����A����ȊO�ɁA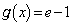 �ƂȂ�x�͂���܂���B
�ƂȂ�x�͂���܂���B
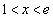 �ɂ�����
�ɂ�����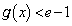 �C
�C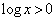 �C
�C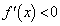
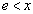 �ɂ�����
�ɂ�����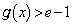 �C
�C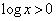 �C
�C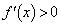
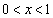 �ɂ�����
�ɂ�����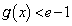 �C
�C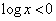 �C
�C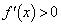
�ȏ���A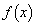 �̑����\�͈ȉ��̂悤�ɂȂ�܂��B
�̑����\�͈ȉ��̂悤�ɂȂ�܂��B
�����\���A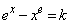 �̐��̉��̌��́A
�̐��̉��̌��́A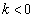 �̂Ƃ�0�C
�̂Ƃ�0�C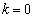 �C
�C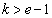 �̂Ƃ�1�C
�̂Ƃ�1�C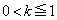 �C
�C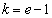 �̂Ƃ�2�C
�̂Ƃ�2�C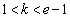 �̂Ƃ�3�� ......[��]
�̂Ƃ�3�� ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B