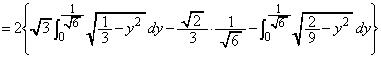���H�吔�w'13�N�O��[5]
a�Cb�𐳂̎����Ƃ��A�~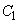 �F
�F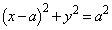 �Ƒȉ~
�Ƒȉ~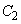 �F
�F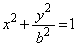 ���l����B
���l����B
(1) 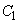 ��
��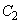 �ɓ��ڂ��邽�߂�a�Cb�̏��������߂�B
�ɓ��ڂ��邽�߂�a�Cb�̏��������߂�B (2) 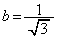 �Ƃ��A
�Ƃ��A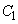 ��
��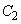 �ɓ��ڂ��Ă���Ƃ���B���̂Ƃ��A��1�ی��ɂ�����
�ɓ��ڂ��Ă���Ƃ���B���̂Ƃ��A��1�ی��ɂ�����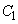 ��
��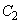 �̐ړ_�̍��W
�̐ړ_�̍��W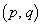 �����߂�B
�����߂�B (3) (2)�̏����̂��ƂŁA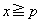 �͈̔͂ɂ����āA
�͈̔͂ɂ����āA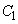 ��
��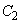 �ň͂܂ꂽ�����̖ʐς����߂�B
�ň͂܂ꂽ�����̖ʐς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�~���ȉ~���ڂ�����́A���嗝�n'96�N�O��[6]�C���H��'98�N���[2]�Ȃǂ̗ޑ肪����܂��B
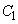 ��
��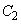 �ɓ��ڂ���Ƃ��A�ȉ~�̎��[�_
�ɓ��ڂ���Ƃ��A�ȉ~�̎��[�_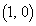 �ɂ����Đڂ���ꍇ�ƁA���[�_�ȊO�̑�1�ی��A��4�ی��ɂ����Đڂ���ꍇ��2�ʂ肪���邱�Ƃɒ��ӂ��܂��B
�ɂ����Đڂ���ꍇ�ƁA���[�_�ȊO�̑�1�ی��A��4�ی��ɂ����Đڂ���ꍇ��2�ʂ肪���邱�Ƃɒ��ӂ��܂��B
(1) 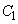 �̎���ό`���āA
�̎���ό`���āA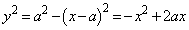 �@����@
�@����@ 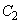 �̎���ό`���āA
�̎���ό`���āA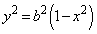 �@����A
�@����A
�@�ƇA��A������ƁA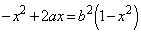
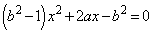 �@����B
�@����B�@��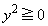 ���~
���~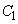 �̑��ݔ͈͂́A
�̑��ݔ͈͂́A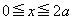 �@����C
�@����C
�A��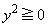 ���ȉ~
���ȉ~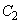 �̑��ݔ͈͂́A
�̑��ݔ͈͂́A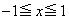 �@����D
�@����D
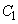 ��
��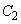 �ɓ��ڂ���̂ŁA�C�͈͇̔͂D�͈̔͂Ɋ܂܂��K�v������܂��B����āA
�ɓ��ڂ���̂ŁA�C�͈͇̔͂D�͈̔͂Ɋ܂܂��K�v������܂��B����āA �����ŁA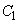 �C
�C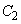 �̐ڂ����ŏꍇ�������܂��B
�̐ڂ����ŏꍇ�������܂��B (i) 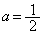 �̂Ƃ��A�~
�̂Ƃ��A�~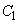 �́A
�́A ��
��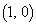 �a�̗��[�Ƃ���~�ɂȂ�܂����A���̂Ƃ��A
�a�̗��[�Ƃ���~�ɂȂ�܂����A���̂Ƃ��A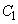 ��
��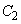 ��
��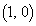 �ɂ����Đڂ��܂��B
�ɂ����Đڂ��܂��B ���̂Ƃ��A�B�́A
����2���������́A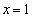 �̂ق��ɁA
�̂ق��ɁA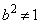 �̂Ƃ��ɂ͌�������
�̂Ƃ��ɂ͌�������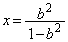 �Ƃ������������Ă��܂��B�~
�Ƃ������������Ă��܂��B�~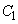 ���~
���~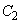 �ɓ��ڂ�������́A2���������B���A�C�͈̔́F
�ɓ��ڂ�������́A2���������B���A�C�͈̔́F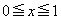 ��
��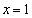 �ȊO�̉��������Ȃ�����(���������Ă��܂��ƁA������
�ȊO�̉��������Ȃ�����(���������Ă��܂��ƁA������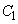 ��
��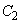 ������邱�ƂɂȂ�܂�)�ł�(2���������̈�ʘ_���Q��)�B�܂�A
������邱�ƂɂȂ�܂�)�ł�(2���������̈�ʘ_���Q��)�B�܂�A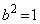 �ƂȂ邩�A�܂��́A
�ƂȂ邩�A�܂��́A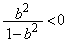 �C�܂��́A
�C�܂��́A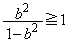
����āA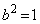 �C�܂��́A
�C�܂��́A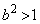 �C�܂��́A
�C�܂��́A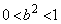 ����
����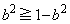
�ȏ���A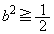
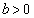 ���A
���A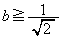
(ii) 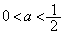 �̂Ƃ��A
�̂Ƃ��A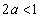 ���A�~
���A�~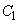 ��
��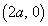 �ɂ�����
�ɂ�����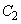 �Ɛڂ��邱�Ƃ͂Ȃ��A�ڂ���Ƃ���A
�Ɛڂ��邱�Ƃ͂Ȃ��A�ڂ���Ƃ���A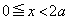 �ɂ����Ăł����āA
�ɂ����Ăł����āA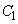 ��
��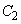 �ɑ�1�ی��A��4�ی��œ��ڂ��܂��B
�ɑ�1�ی��A��4�ی��œ��ڂ��܂��B ���̂Ƃ��́A�~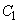 ���~
���~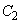 �ɓ��ڂ�������́A2���������B���A�C�͈̔́F
�ɓ��ڂ�������́A2���������B���A�C�͈̔́F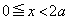 �ɏd���������Ƃł��B
�ɏd���������Ƃł��B �� 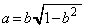 (
(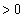 )���̂Ƃ��A�d���́A
)���̂Ƃ��A�d���́A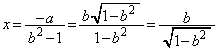
���ꂪ�B�͈̔͂ɑ����邱�Ƃ���A �ȏ���A���߂�����́A
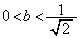 ����
����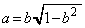 �܂��́A
�܂��́A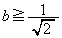 ����
����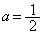 ......[��]
......[��]
(2) 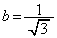 �́A
�́A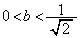 �����̂ŁA���̂Ƃ��A
�����̂ŁA���̂Ƃ��A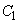 ��
��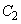 �ɑ�1�ی��A��4�ی��ɂ����ē��ڂ��܂��B
�ɑ�1�ی��A��4�ی��ɂ����ē��ڂ��܂��B (1)���B��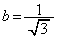 �C
�C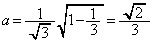 �Ƃ���ƁA
�Ƃ���ƁA �A���A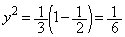 �@��
�@�� 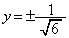
����āA��1�ی��̐ړ_��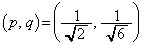 ......[��]
......[��]
(3) �ȉ��A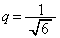 �Ƃ��܂��B���߂�ʐ�S�́A
�Ƃ��܂��B���߂�ʐ�S�́A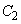 �F
�F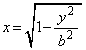 ��
��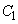 �F
�F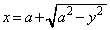 �ɋ��܂ꂽ����(
�ɋ��܂ꂽ����(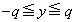 )�̖ʐςŁA
)�̖ʐςŁA �ŏ��̐ϕ��́A���a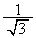 �̉~��
�̉~��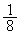 (���p
(���p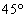 �̐�`)�ƁA���
�̐�`)�ƁA���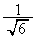 �C����
�C����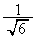 �̎O�p�`�̖ʐς̘a�ł���A�Ō�̐ϕ��́A���a
�̎O�p�`�̖ʐς̘a�ł���A�Ō�̐ϕ��́A���a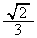 �̉~��
�̉~��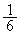 (���p
(���p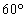 �̐�`)�ƁA���
�̐�`)�ƁA���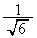 �C����
�C����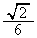 �̎O�p�`�̖ʐς̘a�ɂȂ�܂�(�u���ϕ�(����2)���Q��)�B
�̎O�p�`�̖ʐς̘a�ɂȂ�܂�(�u���ϕ�(����2)���Q��)�B 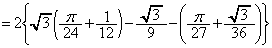
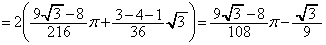 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 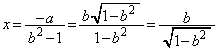
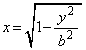 ��
��