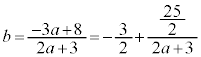���H�吔�w'20�N�O��[3]
���W��Ԃ�5�_
���Ƃ�B����ɁA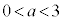 �C
�C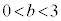 �ɑ���2�_Q
�ɑ���2�_Q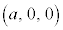 ��R
��R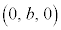 ���l����B
���l����B
(1) �_P�CQ�CR��ʂ镽�ʂ�H�Ƃ���B����H�Ɛ���AC�̌�_T�̍��W�A����ѕ���H�Ɛ���BC�̌�_S�̍��W�����߂�B
(2) �_Q�CR�CS�CT������~����ɂ��邽�߂̕K�v�\��������a�Cb��p���ĕ\���A��������_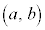 �͈̔͂����W���ʏ�ɐ}������B
�͈̔͂����W���ʏ�ɐ}������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�{��́A��Ԑ}�`�̂܂܍l�@���悤�Ƃ���ƁA���G�ɂȂ�܂��B��Ԑ}�`�̖��ł́A���ʏ�̘b�ōl�@�ł��Ȃ����A�Ƃ������Ƃ��܂��l���܂��B(1)�ł́AT�����߂�Ƃ���xz���ʏ�ŁAS�����߂�Ƃ���yz���ʏ�ōl���܂��B(2)�ł́A��ԏ��4�_�ł͓���ł����A����H��ōl����A�l�p�`���~�ɓ��ڂ�������ł�������܂���B
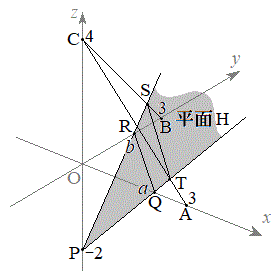
(1) ����H��xz���ʂƂ̌���͒���PQ�ł��B����AC��xz���ʏ�ɂ���̂ŁA��_T��xz���ʏ�ɂ���܂��B�܂�Axz����( )��ŁA����AC�ƒ���PQ�Ƃ̌�_�Ƃ��āAT�̍��W�́A
)��ŁA����AC�ƒ���PQ�Ƃ̌�_�Ƃ��āAT�̍��W�́A T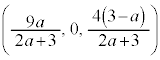 ......[��]�@(
......[��]�@(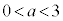 )
) ����H��yz���ʂƂ̌���͒���PR�ł��B����BC��yz���ʏ�ɂ���̂ŁA��_S��yz���ʏ�ɂ���܂��B�܂�Ayz����(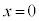 )��ŁA����BC�ƒ���PR�Ƃ̌�_�Ƃ��āAS�̍��W�́A
)��ŁA����BC�ƒ���PR�Ƃ̌�_�Ƃ��āAS�̍��W�́A ����PR�F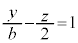 �@����B
�@����B
����BC�F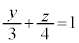 �@����C
�@����C S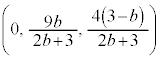 ......[��] �@(
......[��] �@(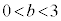 )
)
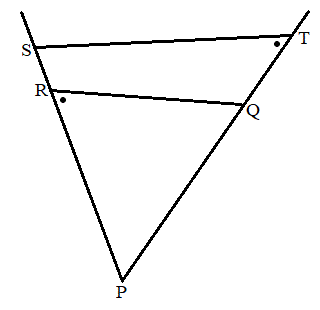 (2) T�CS�́A����H��̓_�Ȃ̂ŁAQ�CR�CS�CT�͂����������H��̓_�ł��B�܂��AP�CQ�CT�͈꒼����(zx���ʂƕ���H�̌����)�AP�CR�CS�͈꒼����(yz���ʂƕ���H�̌����)�ɂ���܂��B����H��ōl����ƁA�l�p�`QRST���~�ɓ��ڂ���K�v�\�������́A
(2) T�CS�́A����H��̓_�Ȃ̂ŁAQ�CR�CS�CT�͂����������H��̓_�ł��B�܂��AP�CQ�CT�͈꒼����(zx���ʂƕ���H�̌����)�AP�CR�CS�͈꒼����(yz���ʂƕ���H�̌����)�ɂ���܂��B����H��ōl����ƁA�l�p�`QRST���~�ɓ��ڂ���K�v�\�������́A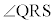 ��
��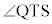 ���݂��ɕ�p���Ȃ����ƁA�ŁA���̂Ƃ��A��PQR�Ɓ�PST�ɂ����āA
���݂��ɕ�p���Ȃ����ƁA�ŁA���̂Ƃ��A��PQR�Ɓ�PST�ɂ����āA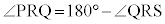 �C
�C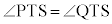 ���
���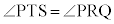 �C�܂�
�C�܂� ���ʂ��A
���ʂ��A��PQR �� ��PST (��p����)
�́@PQ�FPS = PR�FPT�@����D
�D���A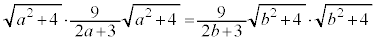
����āA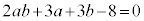 �@����E�C�܂��́A
�@����E�C�܂��́A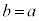 �@(
�@(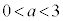 �C
�C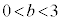 )
)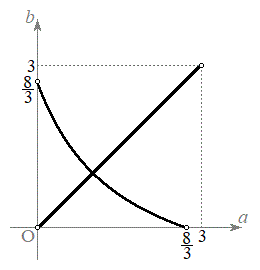 �E�́A
�E�́A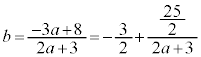
�_Q�CR�CS�CT������~���゠�邽�߂̕K�v�\�������́A
�}������ƁA�E�}����(���}��������)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 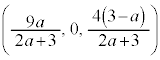 ......[��]�@(
......[��]�@(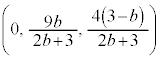 ......[��] �@(
......[��] �@(