東京工業大学2020年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 次の問いに答えよ。
(1) 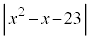 の値が、3を法として2に合同である正の整数xをすべて求めよ。
の値が、3を法として2に合同である正の整数xをすべて求めよ。 (2) k個の連続した正の整数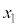 ,・・・,
,・・・,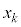 に対して、
に対して、 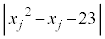 (
(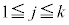 )
)の値がすべて素数になるkの最大値と、そのkに対する連続した正の整数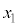 ,・・・,
,・・・,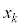 をすべて求めよ。ここでk個の連続した整数とは、
をすべて求めよ。ここでk個の連続した整数とは、 となる列のことである。
[解答へ]
[2] 複素数平面上の異なる3点A,B,Cを複素数α,β,γで表す。ここでA,B,Cは同一直線上にないと仮定する。
(1) △ABCが正三角形となる必要十分条件は、
であることを示せ。
(2) △ABCが正三角形のとき、△ABCの外接円上の点Pを任意にとる。このとき、
および
を外接円の半径Rを用いて表せ。ただし、2点X,Yに対し、XYとは線分XYの長さを表す。
[解答へ]
[3] 座標空間に5点
をとる。さらに、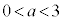 ,
,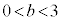 に対して2点Q
に対して2点Q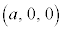 とR
とR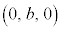 を考える。
を考える。
(1) 点P,Q,Rを通る平面をHとする。平面Hと線分ACの交点Tの座標、および平面Hと線分BCの交点Sの座標を求めよ。
(2) 点Q,R,S,Tが同一円周上あるための必要十分条件をa,bを用いて表し、それを満たす点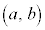 の範囲を座標平面上に図示せよ。
の範囲を座標平面上に図示せよ。 [解答へ]
[4] nを正の奇数とする。曲線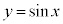 (
(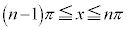 )とx軸で囲まれた部分を
)とx軸で囲まれた部分を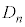 とする。直線
とする。直線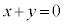 を
を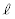 とおき、
とおき、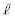 の周りに
の周りに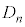 を1回転させてできる回転体を
を1回転させてできる回転体を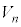 とする。
とする。
(1) 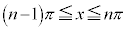 に対して、点
に対して、点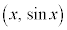 をPとおく。また、Pから
をPとおく。また、Pから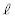 に下ろした垂線とx軸の交点をQとする。線分PQを
に下ろした垂線とx軸の交点をQとする。線分PQを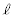 の周りに1回転させてできる図形の面積をxの式で表せ。
の周りに1回転させてできる図形の面積をxの式で表せ。 (2) (1)の結果を用いて、回転体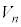 の体積をnの式で表せ。
の体積をnの式で表せ。 [解答へ]
[5] kを正の整数とし、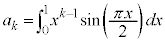 とおく。
とおく。
(1) 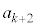 を
を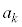 とkを用いて表せ。
とkを用いて表せ。 (2) kを限りなく大きくするとき、数列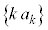 の極限値Aを求めよ。
の極限値Aを求めよ。 (3) (2)の極限値Aに対し、kを限りなく大きくするとき、数列
が0ではない値に収束する整数m,n (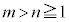 )を求めよ。また、そのときの極限値Bを求めよ。
)を求めよ。また、そのときの極限値Bを求めよ。 (4) (2)と(3)の極限値A,Bに対し、kを限りなく大きくするとき、数列
が0ではない値に収束する整数p,q,r (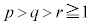 )を求めよ。また、そのときの極限値を求めよ。
)を求めよ。また、そのときの極限値を求めよ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東工大数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。