���H�吔�w'20�N�O��[2]
���f�����ʏ�̈قȂ�3�_A�CB�CC�f��α�Cβ�Cγ�ŕ\���B������A�CB�CC�͓��꒼����ɂȂ��Ɖ��肷��B
(1) ��ABC�����O�p�`�ƂȂ�K�v�\�������́A
�ł��邱�Ƃ������B
(2) ��ABC�����O�p�`�̂Ƃ��A��ABC�̊O�ډ~��̓_P��C�ӂɂƂ�B���̂Ƃ��A
�����
���O�ډ~�̔��aR��p���ĕ\���B�������A2�_X�CY�ɑ��AXY�Ƃ͐���XY�̒�����\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@1��3�捪ω(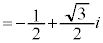 )�̐����A
)�̐����A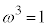 �C
�C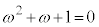 ���t�����p���܂��B
���t�����p���܂��B
(1) ��ӂ̏����̉��ɁA
��ABC�����O�p�` �� �_A�̎���ɓ_B��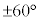 ��]����Ɠ_C
��]����Ɠ_C �� 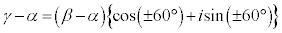
�]���āA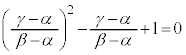 ��
�� 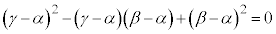 �W�J���Đ�������ƁA
�W�J���Đ�������ƁA 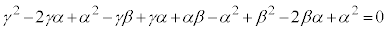 ��
�� 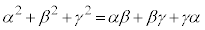
(2) ��ABC�̊O�ډ~�̒��S�����_O�ŁA�~��ɔ����v����A�CB�CC�̏��ɕ���ł���Ƃ��āA��ʐ��������܂���B��ABC�����O�p�`�̂Ƃ��A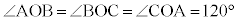 ���A
���A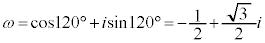 �Ƃ��āA
�Ƃ��āA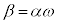 �C
�C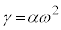 �C
�C �܂��A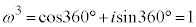 �C
�C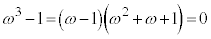 �C
�C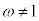 ���A
���A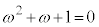 �C
�C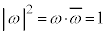 ���A
���A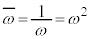 �C
�C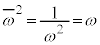 �CP��\�����f����p�Ƃ��āA
�CP��\�����f����p�Ƃ��āA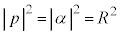 �C�������g���āA
�C�������g���āA 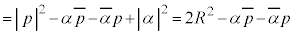 �@����@
�@����@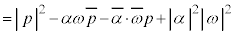
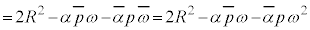 �@����A
�@����A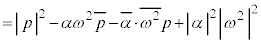
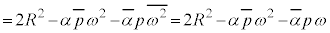 �@����B
�@����B�@�{�A�{�B���A
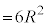 ......[��]
......[��]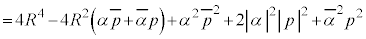
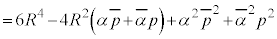 �@����C
�@����C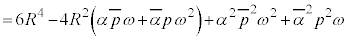 �@����D
�@����D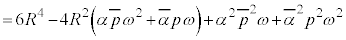 �@����E
�@����E�C�{�D�{�E���A
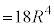 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 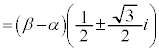
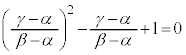 ��
��