東工大数学'20年前期[1]
次の問いに答えよ。
(1) 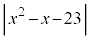の値が、3を法として2に合同である正の整数xをすべて求めよ。
(2) k個の連続した正の整数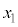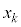，･･･，に対して、
()
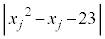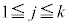の値がすべて素数になるkの最大値と、そのkに対する連続した正の整数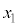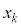，･･･，をすべて求めよ。ここでk個の連続した整数とは、
，，，･･･，
となる列のことである。


【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
 【広告】広告はここまでです。
解答　3を法として2に合同、ということは、3で割って2余るということです。23はどこから来ているのだろう、と、思いますが、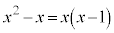の方にカギがありそうです。理論的に迫る方法が見つからないときは、シラミ潰しに調べていきます。

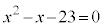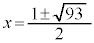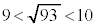(1) とすると、，なので、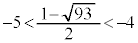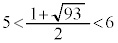，です。絶対値記号の内側が負になる正の整数xの範囲は、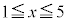
，，，･･･
これで、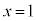とか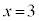が答になる、とわかってしまいます。ならば、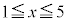より広げ、片っ端から調べて、xに対して、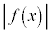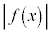，を3で割った余りを表にすると、以下のようになります。
x123456789101112
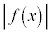23211711371933496787109
3で割った余り202201101101

この表で、ほぼ問題の全容が見えてしまいます。3回に1回の割で3で割った余りが0になり、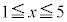の範囲では、3で割り切れるとき以外は余りが2，
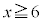の範囲では、3で割り切れるとき以外は余りが1になっているように見えます。
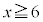の範囲については、確かめておく必要があります。 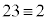(mod. 3) (剰余類を参照)より、
i) 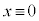(mod. 3)，または、 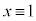(mod. 3)のとき、
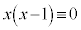(mod. 3)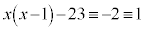， (mod. 3)
ii) 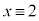(mod. 3)のとき、 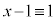(mod. 3)より、
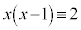(mod. 3)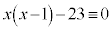， (mod. 3)
これより、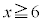のとき、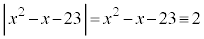 (mod. 3)となることはありません。
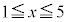については、上記の表より、 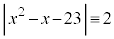(mod. 3)となるのは、
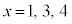......[答] のとき。

(2) (1)の表で、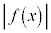の欄に素数が並ぶのは、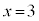から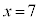までのところで、17，11，3，7，19の5個の素数が並びます。ですが、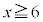においては、(1)(ii)で見たように、3個に1個は3の倍数(xが3で割って2余るとき)なので、5個以上整数が並ぶことはありません。
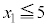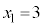つまり、のときは、のとき、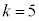が最大となり、k個の連続した正の整数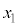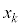，･･･，に対して、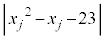 (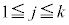)の値17，11，3，7，19はすべて素数です。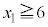の場合は、(1)(ii)により、3個の連続した正の整数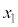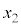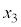，，に対する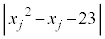 (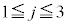)の値のいずれかは3の倍数となり、5個以上素数が続くことはありません。
よって、求めるkの最大値は5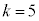，に対する正の整数は、3，4，5，6，7 ......[答]



【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
 【広告】広告はここまでです。
　　東工大数学TOP　　数学TOP　　TOPページに戻る

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。
©2005-2024
(有)りるらる
苦学楽学塾 随時入会受付中！
理系大学受験ネット塾苦学楽学塾
(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。