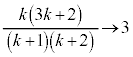���H�吔�w'20�N�O��[5]
k�𐳂̐����Ƃ��A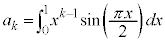 �Ƃ����B
�Ƃ����B
(1) 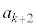 ��
��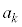 ��k��p���ĕ\���B
��k��p���ĕ\���B (2) k������Ȃ��傫������Ƃ��A����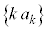 �̋Ɍ��lA�����߂�B
�̋Ɍ��lA�����߂�B (3) (2)�̋Ɍ��lA�ɑ��Ak������Ȃ��傫������Ƃ��A����
��0�ł͂Ȃ��l�Ɏ������鐮��m�Cn (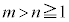 )�����߂�B�܂��A���̂Ƃ��̋Ɍ��lB�����߂�B
)�����߂�B�܂��A���̂Ƃ��̋Ɍ��lB�����߂�B (4) (2)��(3)�̋Ɍ��lA�CB�ɑ��Ak������Ȃ��傫������Ƃ��A����
��0�ł͂Ȃ��l�Ɏ������鐮��p�Cq�Cr (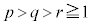 )�����߂�B�܂��A���̂Ƃ��̋Ɍ��l�����߂�B
)�����߂�B�܂��A���̂Ƃ��̋Ɍ��l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ǂ�����v�����̂��낤�A�Ƃ����悤�ȖڐV�������ł����A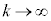 �Ƃ����Ƃ��ɁA0�Ɏ���������̂�k��������0�ȊO�̒l�Ɏ��������A���̋Ɍ��l�������Ƃ܂�0�Ɏ�������̂ŁA�����k�������āA0�ȊO�̒l�Ɏ���������A�Ƃ������ł��B(1)�������ϕ��@�ɂ���Čv�Z���邾���ł����A(2)��(1)�̑Q�������g���āA
�Ƃ����Ƃ��ɁA0�Ɏ���������̂�k��������0�ȊO�̒l�Ɏ��������A���̋Ɍ��l�������Ƃ܂�0�Ɏ�������̂ŁA�����k�������āA0�ȊO�̒l�Ɏ���������A�Ƃ������ł��B(1)�������ϕ��@�ɂ���Čv�Z���邾���ł����A(2)��(1)�̑Q�������g���āA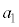 �C
�C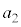 �C
�C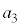 �C
�C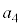 �C��� �Ƃ���čs���ƁA���̐��������ǂ�ǂG�����čs���̂Ŕj�ł��܂��B�����ŁA��蕶���̐ϕ��̎��𗘗p���悤�A�Ƃ������ƂɂȂ�܂����A�������Đϕ��Ɋւ���s�����𗘗p���Ă͂��݂����Ɏ������ރp�^�[���͓��H��ł͂悭�����܂��B
�C��� �Ƃ���čs���ƁA���̐��������ǂ�ǂG�����čs���̂Ŕj�ł��܂��B�����ŁA��蕶���̐ϕ��̎��𗘗p���悤�A�Ƃ������ƂɂȂ�܂����A�������Đϕ��Ɋւ���s�����𗘗p���Ă͂��݂����Ɏ������ރp�^�[���͓��H��ł͂悭�����܂��B
(1) 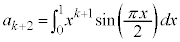
(2) 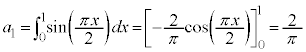
�ȉ��A(1)�ŋ��߂��Q�����𗘗p���āA
�Ƃ�肽���Ȃ�̂ł����A�W�]���������j�ł��҂��Ă��܂��B������ł́A���̕ӂŌ���Ȃ��Ǝ��Ԃ������Ȃ�܂��B(1)�ŋ��߂��Q���������̂܂ܓK�p����̂ł́A�Ɍ��l�����߂�ꂻ�����Ȃ��̂ŁA���̎肪�����T���܂��B�����ŁA��蕶��ǂݒ����ƁA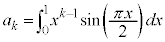 �@����@�@�Ƃ����ϕ��̎��������Ă��܂��B���H��ł́A�͂��݂������p�o�Ȃ̂ŁA�͂��݂����Ɏ������߂Ȃ����A�l���܂��B
�@����@�@�Ƃ����ϕ��̎��������Ă��܂��B���H��ł́A�͂��݂������p�o�Ȃ̂ŁA�͂��݂����Ɏ������߂Ȃ����A�l���܂��B
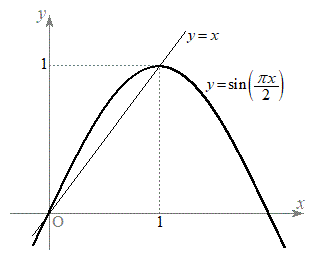
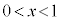 �ɂ����āA
�ɂ����āA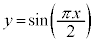 �̃O���t�͏�ɓʂŁA�P���ɑ�������̂ŁA�E�}����A
�̃O���t�͏�ɓʂŁA�P���ɑ�������̂ŁA�E�}����A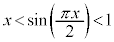 �Ƃ����s�������ł��܂��B
�Ƃ����s�������ł��܂��B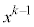 (
(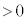 )�������āA
)�������āA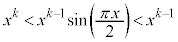 �C�]���āA
�C�]���āA 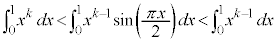 �@����A
�@����A�����ŁA
����ƁA�@�C�A�Ƃ���A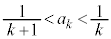 �@����B
�@����B
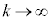 �̂Ƃ��A
�̂Ƃ��A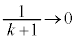 �C
�C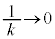 �C�͂��݂����̌������A
�C�͂��݂����̌������A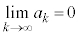 �@����C
�@����C
�B�̊e�ӂ�k�������āA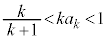 �C
�C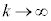 �̂Ƃ��A
�̂Ƃ��A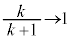 �C�͂��݂����̌������A
�C�͂��݂����̌������A 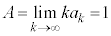 ......[��]
......[��]
(3) (1)�̌��ʂ��A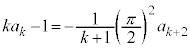 �@����D
�@����D ���ӂ́A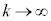 �̂Ƃ��A(2)���A
�̂Ƃ��A(2)���A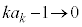 �ł����A�E�ӂ��A�C���A
�ł����A�E�ӂ��A�C���A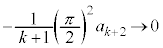 �ł��Bm�Cn�͐����Ȃ̂ŁA�D��k����������Ă����܂��B�܂��A�D��k�������āA
�ł��Bm�Cn�͐����Ȃ̂ŁA�D��k����������Ă����܂��B�܂��A�D��k�������āA 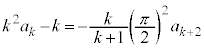 �@����E
�@����E�E�ӂ́A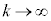 �̂Ƃ��A
�̂Ƃ��A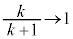 �C�C���
�C�C���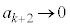 �A����āA
�A����āA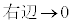 �ŁA
�ŁA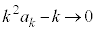
����ɇE��k�������܂��B 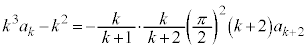 �@����F
�@����F�E�ӂ́A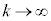 �̂Ƃ��A
�̂Ƃ��A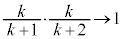 �C(2)���A
�C(2)���A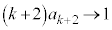
�ȏ���A�F�́A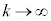 �̂Ƃ��A
�̂Ƃ��A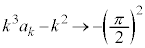 �@(����̋Ɍ����Q��)����āA����
�@(����̋Ɍ����Q��)����āA����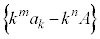 ��0�łȂ��l�Ɏ�������m�Cn (
��0�łȂ��l�Ɏ�������m�Cn (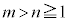 )�́A
)�́A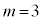 �C
�C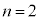 �C�܂��A
�C�܂��A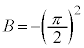 ......[��]
......[��]
(4) (3)�̌��ʂ��A�F�̗��ӂ�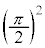 ��������ƁA
��������ƁA
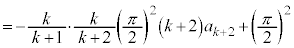 (
(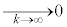 )
)���ӂ�k�������āA�E�ӂ��A�D�̗��p���l���A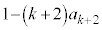 �̌`���o�Ă���悤�ɕό`���܂��B
�̌`���o�Ă���悤�ɕό`���܂��B 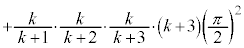
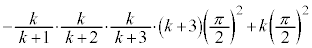 �@(�������̂������Ĉ�����)
�@(�������̂������Ĉ�����)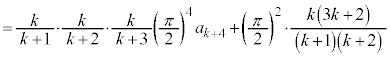 �@(�D�𗘗p���āA
�@(�D�𗘗p���āA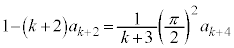 )
)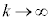 �̂Ƃ��A�C���
�̂Ƃ��A�C���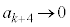 �C�܂��A
�C�܂��A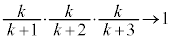 �C
�C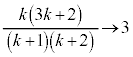
����āA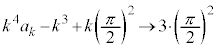 �@(����̋Ɍ����Q��)����
�@(����̋Ɍ����Q��)����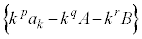 ��0�ł͂Ȃ��l�Ɏ������鐮��p�Cq�Cr (
��0�ł͂Ȃ��l�Ɏ������鐮��p�Cq�Cr (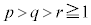 )�́A
)�́A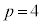 �C
�C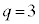 �C
�C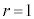 �C�Ɍ��l�́A
�C�Ɍ��l�́A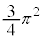 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 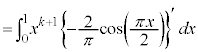
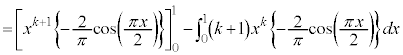
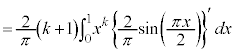
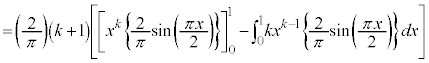
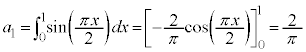
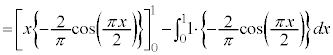
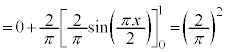
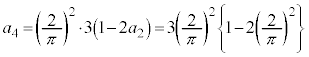
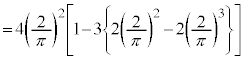
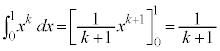
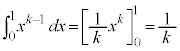
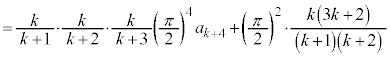 �@(�D�𗘗p���āA
�@(�D�𗘗p���āA