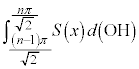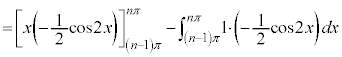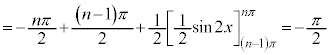���H�吔�w'20�N�O��[4]
n�𐳂̊�Ƃ���B�Ȑ�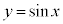 (
(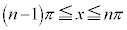 )��x���ň͂܂ꂽ������
)��x���ň͂܂ꂽ������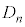 �Ƃ���B����
�Ƃ���B����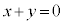 ��
��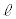 �Ƃ����A
�Ƃ����A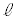 �̎����
�̎����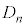 ��1��]�����Ăł����]�̂�
��1��]�����Ăł����]�̂�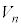 �Ƃ���B
�Ƃ���B
(1) 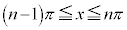 �ɑ��āA�_
�ɑ��āA�_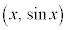 ��P�Ƃ����B�܂��AP����
��P�Ƃ����B�܂��AP����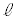 �ɉ��낵��������x���̌�_��Q�Ƃ���B����PQ��
�ɉ��낵��������x���̌�_��Q�Ƃ���B����PQ��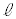 �̎����1��]�����Ăł���}�`�̖ʐς�x�̎��ŕ\���B
�̎����1��]�����Ăł���}�`�̖ʐς�x�̎��ŕ\���B (2) (1)�̌��ʂ�p���āA��]��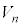 �̑̐ς�n�̎��ŕ\���B
�̑̐ς�n�̎��ŕ\���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Ή�]���̖��ł��B�U�����t���Ă���̂ŁA�������o��������A���ɖ��͂Ȃ��ł��傤�B�v�Z�~�X�ɒ��ӂ��܂��B
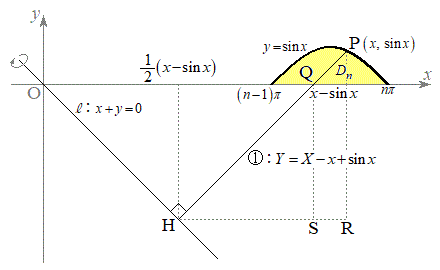
(1) P����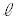 �ɉ��낵�������̑���H�Ƃ��āA���̐����́A�X��1�œ_P
�ɉ��낵�������̑���H�Ƃ��āA���̐����́A�X��1�œ_P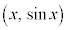 ��ʂ�̂ŁA������̓_��
��ʂ�̂ŁA������̓_��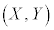 �Ƃ��āA
�Ƃ��āA x���Ƃ̌�_�́A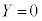 �Ƃ��āA
�Ƃ��āA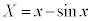 �C�܂�AQ
�C�܂�AQ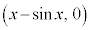
P�CQ�́A���ꂼ��H�𒆐S�Ƃ��āA���aHP�C���aHQ�̉~��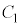 �C
�C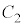 ��`���̂ŁA����PQ��
��`���̂ŁA����PQ��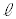 �̎����1��]�����Ăł���}�`�́A���~���ɋ��܂ꂽ�̈�ƂȂ�܂��B
�̎����1��]�����Ăł���}�`�́A���~���ɋ��܂ꂽ�̈�ƂȂ�܂��B
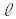 �F
�F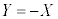 �Ƈ@�̌�_H��x���W�́A������A�����A
�Ƈ@�̌�_H��x���W�́A������A�����A 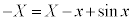 �C
�C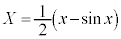 �@����A
�@����AH��ʂ�x���ɕ��s�Ȓ�����P�CQ���牺�낵�������̑����AR�CS�Ƃ���ƁA�E�}�ŁA�����@�̌X����1�Ȃ̂ŁA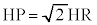 �C
�C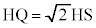 �C����āA
�C����āA ���߂�ʐ�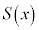 �́A
�́A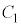 �̖ʐς���
�̖ʐς���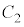 �̖ʐς������āA
�̖ʐς������āA 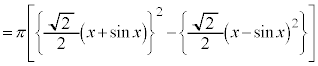
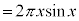 ......[��]
......[��]
(2) (1)�Ŗʐ�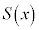 �����߂��}�`�̉�]���͒���
�����߂��}�`�̉�]���͒���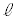 �ł����āAx���ł͂Ȃ��̂ŁA
�ł����āAx���ł͂Ȃ��̂ŁA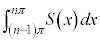 �Ƃ��Ă���]�̂̑̐ς͋��߂��܂���B��]�̂̑̐������߂邽�߂ɂ́A��]�̂̉�]���ɐ����Ȓf�ʂ̖ʐ�
�Ƃ��Ă���]�̂̑̐ς͋��߂��܂���B��]�̂̑̐������߂邽�߂ɂ́A��]�̂̉�]���ɐ����Ȓf�ʂ̖ʐ�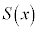 ���A��]��(�{��ł́A����
���A��]��(�{��ł́A����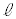 )�ɉ����Đϕ����Ȃ���Ȃ�܂���B
)�ɉ����Đϕ����Ȃ���Ȃ�܂���B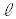 �ɉ����Č��_����̋�����OH�ŁA����PQ�����݂���OH�͈̔͂�
�ɉ����Č��_����̋�����OH�ŁA����PQ�����݂���OH�͈̔͂�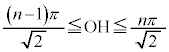 �Ȃ̂ŁA���߂�̐ς́A
�Ȃ̂ŁA���߂�̐ς́A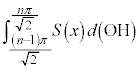 �ƂȂ�܂��B
�ƂȂ�܂��B ���̂܂܂ł́A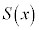 ��OH�Őϕ��ł��Ȃ��̂ŁAOH��x�ŕ\�����u���ϕ����܂��BOH�F
��OH�Őϕ��ł��Ȃ��̂ŁAOH��x�ŕ\�����u���ϕ����܂��BOH�F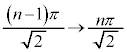 �̂Ƃ�x�F
�̂Ƃ�x�F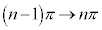 �C�A���A
�C�A���A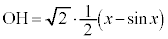 �C
�C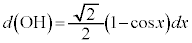
�]���āA ������A
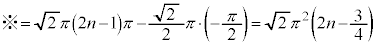 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
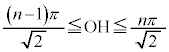 �Ȃ̂ŁA���߂�̐ς́A
�Ȃ̂ŁA���߂�̐ς́A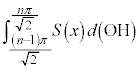 �ƂȂ�܂��B
�ƂȂ�܂��B