���H�吔�w'21�N�O��[4]
S���A���W��ԓ��̌��_O�𒆐S�Ƃ��锼�a1�̋��ʂƂ���BS����_A�CB�CC�CD�ɑ���
�Ƃ����B�ȉ��̖₢�ɓ�����B
(1) 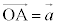 �C
�C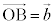 �C
�C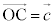 �C
�C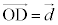 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A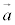 �C
�C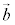 �C
�C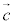 �C
�C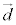 �ɂ��Ȃ��萔k�ɂ����
�ɂ��Ȃ��萔k�ɂ���� �Ə����邱�Ƃ������A�萔k�����߂�B
(2) �_A�CB�CC�CD������S����Ƃ��́AF�̍ő�lM�����߂�B
(3) �_C�̍��W��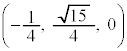 �C�_D�̍��W��
�C�_D�̍��W��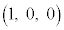 �ł���Ƃ��A
�ł���Ƃ��A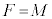 �ƂȂ�S��̓_A�CB�̑g�����ׂċ��߂�B
�ƂȂ�S��̓_A�CB�̑g�����ׂċ��߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�����ς��Ȗ��ŁA���炩�̔w�i������悤�Ɋ����܂����A�Ǖ��ɂ��Ēm��܂���B�Â炸�ɁA�f���Ɍv�Z���čs���Ύ��R�ɃS�[���ɂ��ǂ蒅���܂��B
(2)�ŁA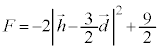 �Ƃ��������o�Ă��܂����A���ꂾ���ł́A
�Ƃ��������o�Ă��܂����A���ꂾ���ł́A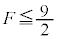 ���K�v�����ƌ����邾���ł��B�u����
���K�v�����ƌ����邾���ł��B�u����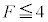 �ł�����
�ł�����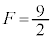 �ƂȂ�ꍇ�����݂��Ȃ��v�A�Ƃ������Ƃ����邩���m��܂���B�uF�̍ő�l��
�ƂȂ�ꍇ�����݂��Ȃ��v�A�Ƃ������Ƃ����邩���m��܂���B�uF�̍ő�l��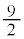 �v���\�������ƌ����邽�߂ɂ́A
�v���\�������ƌ����邽�߂ɂ́A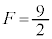 �ɂȂ�̂��ǂ������ꍇ���A�Ƃ������Ƃ����Ȃ�������܂���B���ꂪ(3)�ł�(�����E�������Q��)�B
�ɂȂ�̂��ǂ������ꍇ���A�Ƃ������Ƃ����Ȃ�������܂���B���ꂪ(3)�ł�(�����E�������Q��)�B
A�CB�CC�CD�́A���_O�𒆐S�Ƃ��锼�a1�̋��ʏ�̓_�Ȃ̂ŁA
���l�ɁA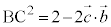 �C
�C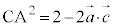 �C
�C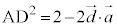 �C
�C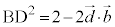 �C
�C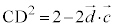 ���A
���A
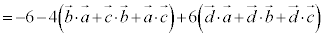 �@����@
�@����@
(1) 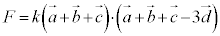 �@����A
�@����A �A�̂悤�����邽�߂ɂ́A�@�Ɣ�r���āA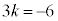 �C
�C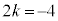 �C
�C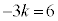 �ł���悭�A
�ł���悭�A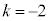 ......[��]
......[��] (2) �A�ɂ����āA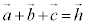 �Ƃ����ƁA
�Ƃ����ƁA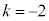 ���A
���A 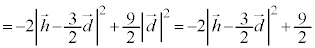 �@����B
�@����B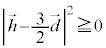 �Ȃ̂ŁA
�Ȃ̂ŁA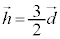 �ƂȂ邱�Ƃ�����A���̂Ƃ�F�ő�ƂȂ�܂����A
�ƂȂ邱�Ƃ�����A���̂Ƃ�F�ő�ƂȂ�܂����A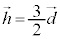 �ƂȂ�Ƃ��A
�ƂȂ�Ƃ��A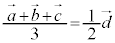 �ł��BOD�̒��_��E�Ƃ��āA��ABC���d�S��E�ɂȂ�܂��B�Ⴆ�AA�CB�CC���AE��ʂ�OD�ɐ����Ȗʂŋ���S������Ƃ��̐���ɂł���~����̓_�ŁA���O�p�`���Ȃ��悤�Ȉʒu�ɂ���A���������ɂȂ�܂��B��̓I�ɏ����ƁAD
�ł��BOD�̒��_��E�Ƃ��āA��ABC���d�S��E�ɂȂ�܂��B�Ⴆ�AA�CB�CC���AE��ʂ�OD�ɐ����Ȗʂŋ���S������Ƃ��̐���ɂł���~����̓_�ŁA���O�p�`���Ȃ��悤�Ȉʒu�ɂ���A���������ɂȂ�܂��B��̓I�ɏ����ƁAD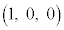 �CE
�CE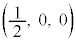 �CA
�CA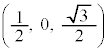 �CB
�CB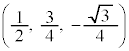 �CC
�CC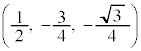 �̂Ƃ��A
�̂Ƃ��A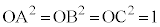 �ł����āA��ABC�̏d�S��E�ɂȂ�܂��B����āA
�ł����āA��ABC�̏d�S��E�ɂȂ�܂��B����āA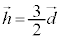 �̂Ƃ��AF�̍ő�l�F
�̂Ƃ��AF�̍ő�l�F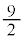 ......[��]
......[��](3) 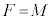 �ƂȂ�Ƃ��A(2)���A
�ƂȂ�Ƃ��A(2)���A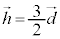 �ƂȂ�܂��B�܂�A
�ƂȂ�܂��B�܂�A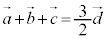
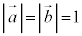 �Ȃ̂ŁA����́A
�Ȃ̂ŁA����́A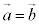 �ł��邱�Ƃ��Ӗ����܂��B
�ł��邱�Ƃ��Ӗ����܂��B
����āA�C���A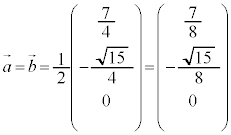 A
A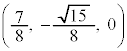 �CB
�CB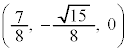 ......[��]
......[��]���D(2)�ŁAF�̍ő�l��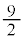 �Ƃ��A(3)�Ř_���܂��A�ƒ��ӏ��������Ă����A�Ƃ����̏����������蓾�܂��B
�Ƃ��A(3)�Ř_���܂��A�ƒ��ӏ��������Ă����A�Ƃ����̏����������蓾�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 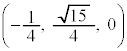 �C�_D�̍��W��
�C�_D�̍��W��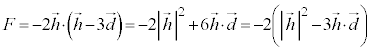
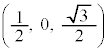 �CB
�CB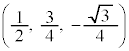 �CC
�CC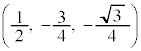 �̂Ƃ��A
�̂Ƃ��A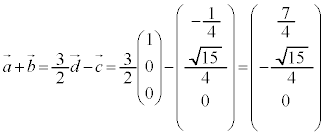 �@����C
�@����C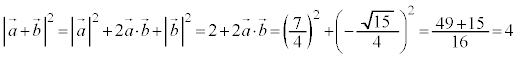
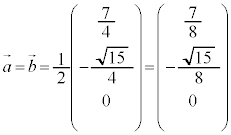
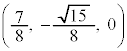 �CB
�CB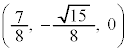 ......[��]
......[��]